Tauche ein in unsere modebewusste Statistik-Welt.
4-Felder-Tafel: bedingte Wahrscheinlichkeit
- Aufbau
- Multiplikationssatz
- bedingte Wahrscheinlichkeit
- Satz der totalen Wahrscheinlichkeit.
- 4-Felder-Tafel füllen
- Wahrscheinlichkeiten berechnen
- Sensitivität und Spezifität
Es hilft euch, wenn ihr bereits den Beitrag zu den Axiomen von Kolmogorow gesehen habt, weil dort viele Grundlagen erklärt werden, die hier relevant sind.
Aufbau der 4-Felder-Tafel
Mit der 4-Felder-Tafel lassen sich absolute bzw. relative Häufigkeiten zweier Ereignisse darstellen. Sie ist äußerst hilfreich in der Wahrscheinlichkeitsrechnung, weil sich viele Aufgaben damit einfacher lösen lassen.
Eine Tafel mit 2 Ereignissen A und B, kann wie folgt aussehen.
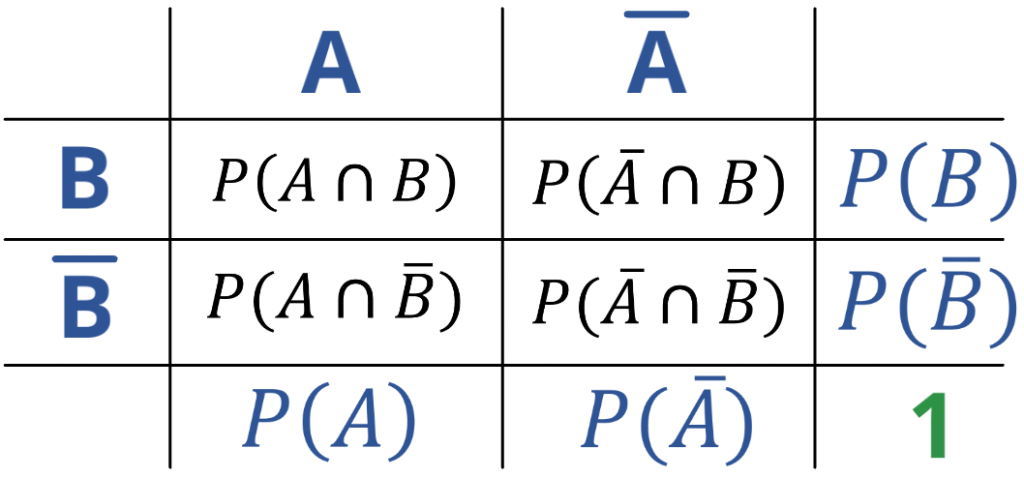
Wir sehen die beiden Ereignisse mit ihren Komplementen. Nochmals zur Erinnerung, die Komplementärereignisse stellen jeweils das Gegenteil unserer Ereignisse dar.
Die 4 inneren Felder der Tafel sind die Felder, wo sich unsere Ereignisse überschneiden. Sie stellen somit die jeweiligen Schnittmengen dar. In dem Feld, wo sich die Ereignisse A und B treffen, haben wir also die Schnittmenge von A und B et. Cetera.
In den Feldern am Rand unserer Tafel stehen die Wahrscheinlichkeiten der jeweiligen Ereignisse. P(A) ist die Wahrscheinlichkeit des Ereignisses A und \(P(\overline{A})\) bzw. \(P(A^c)\) die Gegenwahrscheinlichkeit. Für B ist es natürlich dasselbe. Wir erhalten diese Randwahrscheinlichkeiten jeweils mit dem Satz der vollständigen Wahrscheinlichkeit (dazu gleich noch mehr).
Addiert man P(A) und \(P(A^c)\) bzw. P(B) und \(P(B^c)\) erhalten wir 1 bzw. 100%.
Multiplikationssatz
Der Multiplikationssatz wird verwendet, um die Schnittmenge von abhängigen Ereignissen zu berechnen.
$$\begin{align}P(A \cap B) &= P(A|B) \cdot P(B)\\ &= P(B|A) \cdot P(A) \end{align}$$
Sind die Ereignisse unabhängig, vereinfacht sich die Rechnung zu normalem Multiplizieren.
$$P(A \cap B) = P(A) \cdot P(B)$$
Bedingte Wahrscheinlichkeit
Wenn wir die Wahrscheinlichkeit von A unter der Bedingung von B suchen, haben wir es mit einer bedingten Wahrscheinlichkeit zu tun. Dabei ist der vordere Teil das Ereignis, für das wir die Wahrscheinlichkeit suchen (A) und der hintere Teil die entsprechende Bedingung (B).
$$P(A | B) = \frac{P(A \cap B)}{P(B)}$$
Man rechnet also die Wahrscheinlichkeit der Schnittmenge der beiden Ereignisse durch die Wahrscheinlichkeit für die Bedingung. Man könnte auch sagen „das Bedingungsereignis“.
Vielleicht habt ihr es auch schon gesehen:
Der Multiplikationssatz ist einfach die Formel für die bedingte Wahrscheinlichkeit nur auf die Schnittmenge umgestellt.
Satz der vollständigen Wahrscheinlichkeit
Ein anderer Name ist „der Satz der totalen Wahrscheinlichkeit“, den wir hier für 2 Ereignisse behandeln.
$$P(B) = P(B|A) \cdot P(A) + P(B|A^c) \cdot P(A^c)$$
Mit dem Multiplikationssatz können wir das auch so schreiben:
$$P(B) = P(B \cap A) + P(B \cap A^c)$$
Wenn man sich diese beiden Schnittmengen graphisch vorstellt, macht das ja auch Sinn. Ganz B ergibt sich aus dem Teil von B, der sich mit A schneidet plus dem Teil, der sich mit A-Komplement schneidet.
4-Felder-Tafel befüllen
Als Beispiel haben wir einen Test, der mit 98-prozentiger Wahrscheinlichkeit korrekt erkennt, wenn eine Person krank ist. Zudem erkennt der Test mit 96-prozentiger Wahrscheinlichkeit korrekt, dass eine Person gesund ist. 5% der Personen in unserem Beispiel sind tatsächlich krank.
Zuerst definieren wir unsere Ereignisse. Wir haben also kranke und gesunde Personen, sowie ein positives bzw. negatives Testergebnis.
Die Gegenteile können wir mit Komplementen darstellen. Daher müssen wir lediglich die Ereignisse krank und positiv definieren.
$$K \cdots \text{Person ist krank} \qquad \text{pos} \cdots \text{der Test ist positiv}$$
$$K^c \cdots \text{Person ist gesund} \qquad \text{pos}^c \cdots \text{der Test ist negativ}$$
Ihr könntet natürlich genauso ein G für Gesund bzw. neg für negativ verwenden. Es bleibt euch überlassen, wie ihr eure Variablen definiert.
In der Regel habt ihr bei solchen Aufgaben eine Randwahrscheinlichkeit oder eine Schnittmenge gegeben. Mit dieser Info, fangt ihr am besten an. Wir wissen zum Beispiel, dass 5% der Personen krank sind und somit können wir 0.05 am Rand für die kranken Personen eintragen. Wenn 5% krank sind, können wir gleichzeitig daraus schließen, dass 95% gesund sind, also tragen wir 0.95 daneben ein.
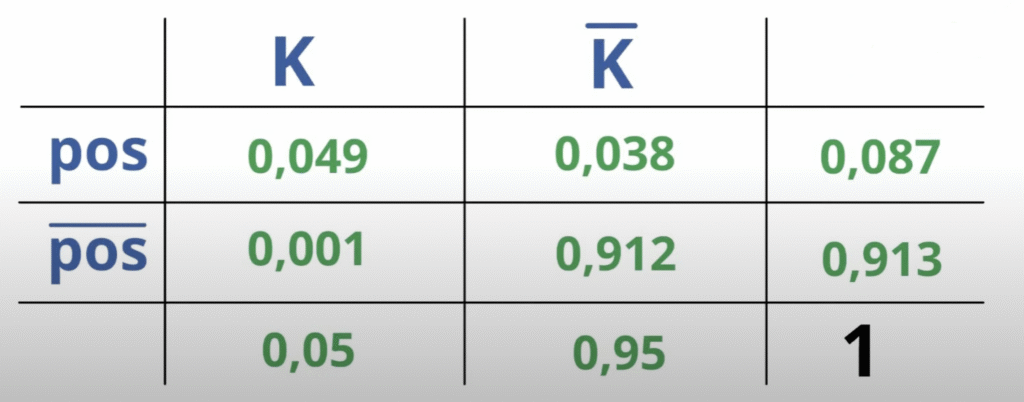
Als Nächstes wissen wir, dass der Test mit 98-prozentiger Wahrscheinlichkeit korrekt eine Krankheit erkennt. Das bezieht sich auf die Schnittmenge von kranken Personen mit positivem Testergebnis (Feld links oben). Wichtig ist aber, dass ihr jetzt nicht einfach die 98% dort eintragt. Diese Wahrscheinlichkeit bezieht sich ja nicht auf alle Personen, sondern lediglich auf die Kranken. Ihr müsst also von den Kranken die 98% berechnen.
$$P(K \cap pos) = 0.05 \cdot 0.98 = 0.049$$
Das Feld darunter ist dann wieder einfach. Eine Person ist krank und hat ein positives Ergebnis und eine Person ist krank und hat ein negatives Ergebnis haben gemeinsam (eine Person ist krank) eine Wahrscheinlichkeit von 5%. Daher kann man subtrahieren, um die Wahrscheinlichkeit, dass eine Person krank ist und ein negatives Ergebnis hat, zu berechnen.
$$P(K \cap pos^c) = 0.05 – 0.049 = 0.001 $$
Wir wissen noch, dass der Test bei gesunden Personen zu 96% richtig liegt. Wenn der Test korrekt ist, heißt das, er muss bei einer gesunden Person negativ sein. Das heißt, es geht hier jetzt um das rechte untere Feld (gesund und negativ). Wir müssen also von den Gesunden 96% bestimmen
$$P(K^c \cap pos^c) = 0.95 \cdot 0.96 = 0.912$$
Nach derselben Logik wie oben, erhalten wir den letzten inneren Wert durch subtrahieren.
$$P(K^c \cap pos) = 0.95 – 0.912 = 0.038$$
Die beiden Randwahrscheinlichkeiten für positiv und negativ erhalten wir dann einfach, indem wir die Werte der jeweiligen Zeilen addieren.
$$P(pos) = 0.049 + 0.038 = 0.087$$
$$P(pos^c) = 0.0091 + 0.012 = 0.913$$
Um zu kontrollieren, dass wir richtig gerechnet haben, schauen wir, ob in der rechten unteren Ecke wirklich 1 herauskommt.
$$P(K) + P(K^c) = 0.05 + 0.95 = 1$$
$$P(pos) + P(neg) = 0.087 + 0.913 = 1$$
Beispiele, Wahrscheinlichkeiten zu berechnen
a) Was ist die Wahrscheinlichkeit für ein positives Testergebnis?
Das ist in diesem Fall sehr simpel, weil wir die ganze Arbeit schon erledigt haben. Wir können den Wert ganz einfach in der entsprechenden Zelle ablesen.
$$ P(pos) = 0.087$$
Aber sehen wir uns etwas genauer an, was da eigentlich dahinter steckt. Die Lösung dafür haben wir zuvor mit dem Satz der totalen Wahrscheinlichkeit berechnet. Wie zuvor erwähnt ist das die Formel:
$$P(B) = P(B \cap A) + P(B \cap A^c)$$
Wir haben für das Ergebnis zuvor 0.049 und 0.038 addiert. Das waren ja nichts anderes als die beiden Schnittmengen von K und pos sowie \(K^c\) und pos. Somit verwendet ihr bei der 4 Felder Tafel, wenn ihr eine Randwahrscheinlichkeit berechnet, automatisch den Satz der totalen Wahrscheinlichkeit, ohne dass es einem wirklich auffällt.
b) Wie hoch ist die Wahrscheinlichkeit, dass eine Person mit positivem Testergebnis tatsächlich krank ist?
Es ist also schon ein Ereignis eingetreten. Und zwar wissen wir, dass die Person ein positives Testergebnis hat. So erkennt ihr, dass es sich hier um eine bedingte Wahrscheinlichkeit handelt. Wichtig ist, dass ihr das Ereignis, dessen Wahrscheinlichkeit wir suchen und das Bedingungsereignis richtig hinschreibt. Wir wollen jetzt die Wahrscheinlichkeit berechnen, dass jemand krank ist, wenn das Testergebnis positiv war. Krank ist das Ereignis, dessen Wahrscheinlichkeit wir suchen und der positive Test das Bedingungsereignis.
$$P(K | pos)$$
Vervollständigen wir die Formel
$$P(K | pos) = \frac{P(K \cap pos)}{P(pos)}$$
Die Schnittmenge ist 0.049 und die Wahrscheinlichkeit von pos ist 0.087.
$$P(K | pos) = \frac{0.049}{0.087} = 0.5632$$
Das heißt also, wenn ich einen positiven Test bekommen habe, dann liegt die Wahrscheinlichkeit, dass ich tatsächlich krank bin bei etwas mehr als 56%.
c) Was ist die Wahrscheinlichkeit, dass jemand krank ist und einen positiven Test hat?
Das klingt fast wie Punkt b) jedoch gibt es hier sehr wichtigen Unterschied. Und zwar wollen wir jetzt krank UND positiv berechnen. Zuvor war es, krank WENN positiv. Aus dem Beitrag zu den Axiomen der Wahrscheinlichkeit wissen wir bereits, dass man mit „und“ die Schnittmenge meint. Die Wahrscheinlichkeit der Schnittmenge von K und pos kennen wir ja mittlerweile. Wir können sie direkt aus der Tafel ablesen und die Lösung ist 0.049.
Auch hier haben wir eine der anfangs erwähnten Formeln bereits verwendet. Den Multiplikationssatz.
$$P(A \cap B) = P(A|B) \cdot P(B)$$
Setzen wir in die Formel ein:
$$P(K \cap pos) = P(pos | K) \cdot P(K)$$
Die Wahrscheinlichkeit von positiv gegeben krank und die Wahrscheinlichkeit von krank hatten wir in der Angabe, das waren 0.98 bzw. 0.05. So haben wir am Anfang des Befüllens der Tabelle mit \(0.98 \cdot 0,05\) die 0.049 erhalten. Ihr seht also, dass ihr alle Formeln von vorhin auch tatsächlich anwendet.
Sensitivität und Spezifität
Diese beiden Begriffe kommen im Zuge von Tests und bei 4-Felder-Tafeln immer wieder vor.
Sensitivität ist einfach ausgedrückt korrekt positiv. Die Sensitivität beschreibt also die Wahrscheinlichkeit, dass der Test positiv ist, wenn die Person krank ist. Das wäre also \(P( pos | K)\). Diese Wahrscheinlichkeit hatten wir anfangs gegeben. Unser Test ist mit 98-prozentiger korrekt, wenn die Person krank war. Somit ist die Sensitivität in diesem Beispiel 0.98.
Die Spezifität ist korrekt negativ, beschreibt also die Wahrscheinlichkeit, dass der Test negativ ist, wenn die Person gesund ist. Also \(P({pos}^c | K^c) \). Auch diesen Wert hatten wir Anfangs gegeben. Unser Test lag mit 96% richtig, wenn die Person gesund ist. Also ist die Spezifität in unserem Beispiel 0.96.
4-Felder-Tafel: bedingte Wahrscheinlichkeit
- Aufbau
- Multiplikationssatz
- bedingte Wahrscheinlichkeit
- Satz der totalen Wahrscheinlichkeit.
- 4-Felder-Tafel füllen
- Wahrscheinlichkeiten berechnen
- Sensitivität und Spezifität
Es hilft euch, wenn ihr bereits den Beitrag zu den Axiomen von Kolmogorow gesehen habt, weil dort viele Grundlagen erklärt werden, die hier relevant sind.
Aufbau der 4-Felder-Tafel
Mit der 4-Felder-Tafel lassen sich absolute bzw. relative Häufigkeiten zweier Ereignisse darstellen. Sie ist äußerst hilfreich in der Wahrscheinlichkeitsrechnung, weil sich viele Aufgaben damit einfacher lösen lassen.
Eine Tafel mit 2 Ereignissen A und B, kann wie folgt aussehen.
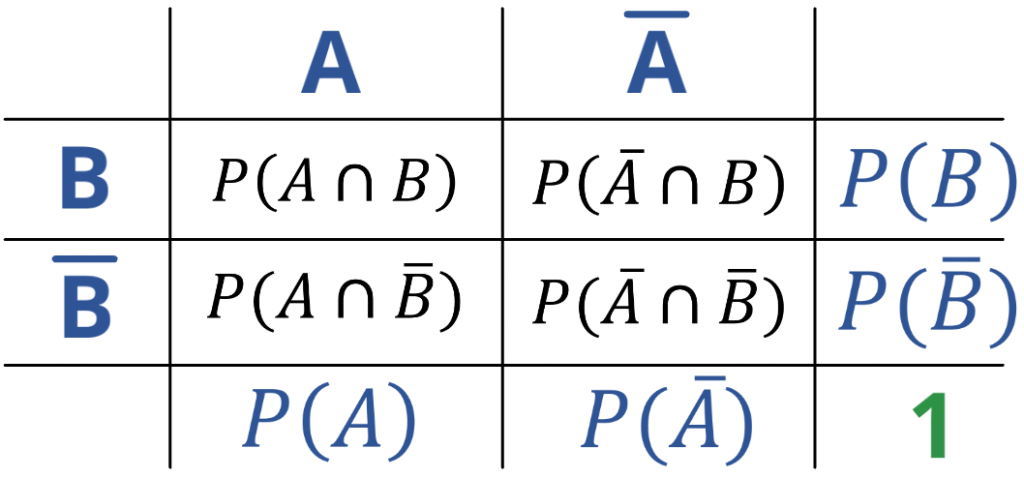
Wir sehen die beiden Ereignisse mit ihren Komplementen. Nochmals zur Erinnerung, die Komplementärereignisse stellen jeweils das Gegenteil unserer Ereignisse dar.
Die 4 inneren Felder der Tafel sind die Felder, wo sich unsere Ereignisse überschneiden. Sie stellen somit die jeweiligen Schnittmengen dar. In dem Feld, wo sich die Ereignisse A und B treffen, haben wir also die Schnittmenge von A und B et. Cetera.
In den Feldern am Rand unserer Tafel stehen die Wahrscheinlichkeiten der jeweiligen Ereignisse. P(A) ist die Wahrscheinlichkeit des Ereignisses A und \(P(\overline{A})\) bzw. \(P(A^c)\) die Gegenwahrscheinlichkeit. Für B ist es natürlich dasselbe. Wir erhalten diese Randwahrscheinlichkeiten jeweils mit dem Satz der vollständigen Wahrscheinlichkeit (dazu gleich noch mehr).
Addiert man P(A) und \(P(A^c)\) bzw. P(B) und \(P(B^c)\) erhalten wir 1 bzw. 100%.
Multiplikationssatz
Der Multiplikationssatz wird verwendet, um die Schnittmenge von abhängigen Ereignissen zu berechnen.
$$\begin{align}P(A \cap B) &= P(A|B) \cdot P(B)\\ &= P(B|A) \cdot P(A) \end{align}$$
Sind die Ereignisse unabhängig, vereinfacht sich die Rechnung zu normalem Multiplizieren.
$$P(A \cap B) = P(A) \cdot P(B)$$
Bedingte Wahrscheinlichkeit
Wenn wir die Wahrscheinlichkeit von A unter der Bedingung von B suchen, haben wir es mit einer bedingten Wahrscheinlichkeit zu tun. Dabei ist der vordere Teil das Ereignis, für das wir die Wahrscheinlichkeit suchen (A) und der hintere Teil die entsprechende Bedingung (B).
$$P(A | B) = \frac{P(A \cap B)}{P(B)}$$
Man rechnet also die Wahrscheinlichkeit der Schnittmenge der beiden Ereignisse durch die Wahrscheinlichkeit für die Bedingung. Man könnte auch sagen „das Bedingungsereignis“.
Vielleicht habt ihr es auch schon gesehen:
Der Multiplikationssatz ist einfach die Formel für die bedingte Wahrscheinlichkeit nur auf die Schnittmenge umgestellt.
Satz der vollständigen Wahrscheinlichkeit
Ein anderer Name ist „der Satz der totalen Wahrscheinlichkeit“, den wir hier für 2 Ereignisse behandeln.
$$P(B) = P(B|A) \cdot P(A) + P(B|A^c) \cdot P(A^c)$$
Mit dem Multiplikationssatz können wir das auch so schreiben:
$$P(B) = P(B \cap A) + P(B \cap A^c)$$
Wenn man sich diese beiden Schnittmengen graphisch vorstellt, macht das ja auch Sinn. Ganz B ergibt sich aus dem Teil von B, der sich mit A schneidet plus dem Teil, der sich mit A-Komplement schneidet.
4-Felder-Tafel befüllen
Als Beispiel haben wir einen Test, der mit 98-prozentiger Wahrscheinlichkeit korrekt erkennt, wenn eine Person krank ist. Zudem erkennt der Test mit 96-prozentiger Wahrscheinlichkeit korrekt, dass eine Person gesund ist. 5% der Personen in unserem Beispiel sind tatsächlich krank.
Zuerst definieren wir unsere Ereignisse. Wir haben also kranke und gesunde Personen, sowie ein positives bzw. negatives Testergebnis.
Die Gegenteile können wir mit Komplementen darstellen. Daher müssen wir lediglich die Ereignisse krank und positiv definieren.
$$K \cdots \text{Person ist krank} \qquad \text{pos} \cdots \text{der Test ist positiv}$$
$$K^c \cdots \text{Person ist gesund} \qquad \text{pos}^c \cdots \text{der Test ist negativ}$$
Ihr könntet natürlich genauso ein G für Gesund bzw. neg für negativ verwenden. Es bleibt euch überlassen, wie ihr eure Variablen definiert.
In der Regel habt ihr bei solchen Aufgaben eine Randwahrscheinlichkeit oder eine Schnittmenge gegeben. Mit dieser Info, fangt ihr am besten an. Wir wissen zum Beispiel, dass 5% der Personen krank sind und somit können wir 0.05 am Rand für die kranken Personen eintragen. Wenn 5% krank sind, können wir gleichzeitig daraus schließen, dass 95% gesund sind, also tragen wir 0.95 daneben ein.

Als Nächstes wissen wir, dass der Test mit 98-prozentiger Wahrscheinlichkeit korrekt eine Krankheit erkennt. Das bezieht sich auf die Schnittmenge von kranken Personen mit positivem Testergebnis (Feld links oben). Wichtig ist aber, dass ihr jetzt nicht einfach die 98% dort eintragt. Diese Wahrscheinlichkeit bezieht sich ja nicht auf alle Personen, sondern lediglich auf die Kranken. Ihr müsst also von den Kranken die 98% berechnen.
$$P(K \cap pos) = 0.05 \cdot 0.98 = 0.049$$
Das Feld darunter ist dann wieder einfach. Eine Person ist krank und hat ein positives Ergebnis und eine Person ist krank und hat ein negatives Ergebnis haben gemeinsam (eine Person ist krank) eine Wahrscheinlichkeit von 5%. Daher kann man subtrahieren, um die Wahrscheinlichkeit, dass eine Person krank ist und ein negatives Ergebnis hat, zu berechnen.
$$P(K \cap pos^c) = 0.05 – 0.049 = 0.001 $$
Wir wissen noch, dass der Test bei gesunden Personen zu 96% richtig liegt. Wenn der Test korrekt ist, heißt das, er muss bei einer gesunden Person negativ sein. Das heißt, es geht hier jetzt um das rechte untere Feld (gesund und negativ). Wir müssen also von den Gesunden 96% bestimmen
$$P(K^c \cap pos^c) = 0.95 \cdot 0.96 = 0.912$$
Nach derselben Logik wie oben, erhalten wir den letzten inneren Wert durch subtrahieren.
$$P(K^c \cap pos) = 0.95 – 0.912 = 0.038$$
Die beiden Randwahrscheinlichkeiten für positiv und negativ erhalten wir dann einfach, indem wir die Werte der jeweiligen Zeilen addieren.
$$P(pos) = 0.049 + 0.038 = 0.087$$
$$P(pos^c) = 0.0091 + 0.012 = 0.913$$
Um zu kontrollieren, dass wir richtig gerechnet haben, schauen wir, ob in der rechten unteren Ecke wirklich 1 herauskommt.
$$P(K) + P(K^c) = 0.05 + 0.95 = 1$$
$$P(pos) + P(neg) = 0.087 + 0.913 = 1$$
Beispiele, Wahrscheinlichkeiten zu berechnen
a) Was ist die Wahrscheinlichkeit für ein positives Testergebnis?
Das ist in diesem Fall sehr simpel, weil wir die ganze Arbeit schon erledigt haben. Wir können den Wert ganz einfach in der entsprechenden Zelle ablesen.
$$ P(pos) = 0.087$$
Aber sehen wir uns etwas genauer an, was da eigentlich dahinter steckt. Die Lösung dafür haben wir zuvor mit dem Satz der totalen Wahrscheinlichkeit berechnet. Wie zuvor erwähnt ist das die Formel:
$$P(B) = P(B \cap A) + P(B \cap A^c)$$
Wir haben für das Ergebnis zuvor 0.049 und 0.038 addiert. Das waren ja nichts anderes als die beiden Schnittmengen von K und pos sowie \(K^c\) und pos. Somit verwendet ihr bei der 4 Felder Tafel, wenn ihr eine Randwahrscheinlichkeit berechnet, automatisch den Satz der totalen Wahrscheinlichkeit, ohne dass es einem wirklich auffällt.
b) Wie hoch ist die Wahrscheinlichkeit, dass eine Person mit positivem Testergebnis tatsächlich krank ist?
Es ist also schon ein Ereignis eingetreten. Und zwar wissen wir, dass die Person ein positives Testergebnis hat. So erkennt ihr, dass es sich hier um eine bedingte Wahrscheinlichkeit handelt. Wichtig ist, dass ihr das Ereignis, dessen Wahrscheinlichkeit wir suchen und das Bedingungsereignis richtig hinschreibt. Wir wollen jetzt die Wahrscheinlichkeit berechnen, dass jemand krank ist, wenn das Testergebnis positiv war. Krank ist das Ereignis, dessen Wahrscheinlichkeit wir suchen und der positive Test das Bedingungsereignis.
$$P(K | pos)$$
Vervollständigen wir die Formel
$$P(K | pos) = \frac{P(K \cap pos)}{P(pos)}$$
Die Schnittmenge ist 0.049 und die Wahrscheinlichkeit von pos ist 0.087.
$$P(K | pos) = \frac{0.049}{0.087} = 0.5632$$
Das heißt also, wenn ich einen positiven Test bekommen habe, dann liegt die Wahrscheinlichkeit, dass ich tatsächlich krank bin bei etwas mehr als 56%.
c) Was ist die Wahrscheinlichkeit, dass jemand krank ist und einen positiven Test hat?
Das klingt fast wie Punkt b) jedoch gibt es hier sehr wichtigen Unterschied. Und zwar wollen wir jetzt krank UND positiv berechnen. Zuvor war es, krank WENN positiv. Aus dem Beitrag zu den Axiomen der Wahrscheinlichkeit wissen wir bereits, dass man mit „und“ die Schnittmenge meint. Die Wahrscheinlichkeit der Schnittmenge von K und pos kennen wir ja mittlerweile. Wir können sie direkt aus der Tafel ablesen und die Lösung ist 0.049.
Auch hier haben wir eine der anfangs erwähnten Formeln bereits verwendet. Den Multiplikationssatz.
$$P(A \cap B) = P(A|B) \cdot P(B)$$
Setzen wir in die Formel ein:
$$P(K \cap pos) = P(pos | K) \cdot P(K)$$
Die Wahrscheinlichkeit von positiv gegeben krank und die Wahrscheinlichkeit von krank hatten wir in der Angabe, das waren 0.98 bzw. 0.05. So haben wir am Anfang des Befüllens der Tabelle mit \(0.98 \cdot 0,05\) die 0.049 erhalten. Ihr seht also, dass ihr alle Formeln von vorhin auch tatsächlich anwendet.
Sensitivität und Spezifität
Diese beiden Begriffe kommen im Zuge von Tests und bei 4-Felder-Tafeln immer wieder vor.
Sensitivität ist einfach ausgedrückt korrekt positiv. Die Sensitivität beschreibt also die Wahrscheinlichkeit, dass der Test positiv ist, wenn die Person krank ist. Das wäre also \(P( pos | K)\). Diese Wahrscheinlichkeit hatten wir anfangs gegeben. Unser Test ist mit 98-prozentiger korrekt, wenn die Person krank war. Somit ist die Sensitivität in diesem Beispiel 0.98.
Die Spezifität ist korrekt negativ, beschreibt also die Wahrscheinlichkeit, dass der Test negativ ist, wenn die Person gesund ist. Also \(P({pos}^c | K^c) \). Auch diesen Wert hatten wir Anfangs gegeben. Unser Test lag mit 96% richtig, wenn die Person gesund ist. Also ist die Spezifität in unserem Beispiel 0.96.

Comments (2)
[…] es euch, wenn ihr bereits mit den Axiomen von Kolmogorov, der Laplace Wahrscheinlichkeit und der 4-Felder-Tafel vertraut […]
You know how we used to make up nonsense words as kids?
We’d string together random sounds just for fun—no rules, no logic.
Well…
turns out that same skill is now worth serious money.
I’m talking about people getting paid thousands just for inventing made up
words!
I’m serious…just by coming up with made up words…words that mean nothing.
There is only one condition:
they have to be 4 or 5 letters (EASY!)
No business. No followers. No nothing.
Just something most of us were naturally good at when we were
6.
Watch this quick video and see how it works : https://jvz1.com/c/688203/418319/