Tauche ein in unsere modebewusste Statistik-Welt.
Konfidenzintervall für Erwartungswert
In diesem Beitrag besprechen wir die Berechnung von Konfidenzintervallen für den Erwartungswert bei einer Stichprobe.
- Punktschätzer und Quantil bestimmen
- T-Verteilung bzw. Normalverteilung
- Konfidenzintervall berechnen
- Interpretation
Die Grundlagen zu Konfidenzintervallen werden im Beitrag Konfidenzintervalle – Erklärung genauer beschrieben. Das Wissen in diesem Beitrag wird hier vorausgesetzt.
Was ist ein Konfidenzintervall?
Ein Konfidenzintervall, auch Vertrauensintervall genannt, ist eine Schätzung für einen unbekannten Parameter. Es gibt einen Bereich an, in dem sich dieser unbekannte Parameter mit einer gewissen Sicherheit befinden soll. Konfidenzintervalle, auch wenn sie teilweise sehr unterschiedlich aussehen, sind im Allgemeinen gleich aufgebaut:
[Punktschätzer ± Quantil * Standardfehler]
Ein Konfidenzintervall für den Erwartungswert schaut so aus:
$$ [{\color{#2dacb4}{\bar{x}} \pm \color{#fc7a7a}{t_{1-\frac{\alpha}{2};df}}*\color{
#3094d4}{\frac{s}{\sqrt{n}}}} ]$$
Beim Konfidenzintervall für den Erwartungswert ist der Punktschätzer einfach der Mittelwert der Stichprobe. \(\bar{x}\).
Für das Quantil verwenden wir in der Regel die T-Verteilung und den Standardfehler erhalten wir, indem wir die Standardabweichung durch die Wurzel von n dividieren.
Hier ist wichtig, dass ihr die geschätzte Populationsstandardabweichung verwendet. Bei dieser wird durch n-1 anstatt durch n dividiert. Sie wird auch häufig mit \(\widehat{\sigma}\) abgekürzt.
Quantil bestimmen
Um dieses Konfidenzintervall bestimmen zu können, muss die Grundgesamtheit normalverteilt sein. Für die Berechnung ist wichtig, ob die Varianz der Population bekannt ist oder nicht.
Bei unbekannter Varianz verwenden wir in der Regel das Quantil der T-Verteilung.
Die T-Verteilung nähert sich mit wachsender Anzahl der Freiheitsgrade an die Standardnormalverteilung an.
Daher kann die T-Verteilung auch durch die Normalverteilung approximiert werden, wenn die Anzahl an Freiheitsgraden groß genug ist und wir können dann das Quantil der Standardnormalverteilung verwenden.
Welche Anzahl an Freiheitsgraden „groß genug“ ist, ist je nach Quelle unterschiedlich. Meistens wird der Wert 30 genannt. Das heißt also, wenn die Freiheitsgrade kleiner gleich 30 sind, verwenden wir das Quantil der T-Verteilung in unserem Konfidenzintervall.
$$df \leq 30: \quad [\bar{x} \pm t_{1-\frac{\alpha}{2};df} \cdot \frac{s}{\sqrt{n}}]$$
Wenn die Freiheitsgrade über 30 liegen, nehmen wir das Quantil der Standardnormalverteilung.
$$df \geq 30: \quad [\bar{x} \pm z_{1-\frac{\alpha}{2}} \cdot \frac{s}{\sqrt{n}}]$$
Auf Englisch heißen Freiheitsgrade übrigens degrees of freedom weswegen wir sie mit df abkürzen. Bitte beachtet, dass es nur eine grobe Orientierung ist, zu sagen, die Approximation der T-Verteilung durch die Normalverteilung wäre ab 30 Freiheitsgraden gut genug. Es gibt auch Quellen, die eine Annäherung erst ab 50 bzw. 100 Freiheitsgraden als ausreichend gut sehen.
Wann ihr die T- oder die Normalverteilungstabelle nehmt, kommt also darauf an, ab wann ihr Approximation der T-Verteilung durch die Normalverteilung für gut genug haltet. Am einfachsten ist, ihr verwendet die Tabelle zur T-Verteilung, die ihr von eurer Schule oder Uni bekommen habt und sobald die gegebenen Freiheitsgrade die Freiheitsgrade in eurer Tabelle überschreiten, verwendet ihr das Quantil der Normalverteilung.
Wenn die Varianz der Grundgesamtheit bekannt ist, dann verwenden wir das Quantil der Standardnormalverteilung und im Standardfehler dividieren wir nun die Populationsstandardabweichung durch den Stichprobenumfang.
$$\text{Varianz bekannt: } \quad [\bar{x} \pm z_{1-\frac{\alpha}{2}} \cdot \frac{\sigma}{n}]$$
Wie ihr aus dem Beitrag Konfidenzintervalle – Erklärung schon wisst, verwenden wir für Populationsparameter griechische Buchstaben – deswegen \(\sigma\).
In diesem Video werden wir nur auf den Fall der unbekannten Varianz eingehen.
Beispiel zur Berechnung
Für die Berechnung gehen wir davon aus, dass wir eine Firma haben und die durchschnittlichen Ausgaben unserer Kunden bestimmen wollen. Dafür haben wir eine Stichprobe von 20 Personen gezogen, wobei die mittleren Ausgaben dieser bei 53.1€ und die Standardabweichung bei 9.3€ liegen. Wir können davon ausgehen, dass die Ausgaben in der Grundgesamtheit normalverteilt sind und wir wollen nun das 99% Konfidenzintervall für den unbekannten Erwartungswert bestimmen.
$$\bar{x} = 53.1 \quad s = 9.3 \quad n = 20$$
Die Varianz der Grundgesamtheit ist also nicht bekannt. (Nur die Varianz der Stichprobe)
Wir haben zuvor schon erwähnt, dass die Wahl des Quantils von der Anzahl der Freiheitsgrade abhängt. In diesem Fall liegen uns n-1 Freiheitsgrade vor.
$$df = n-1 = 20 -1 = 19$$
Da wir 19 Freiheitsgrade haben, verwenden wir das Quantil der T-Verteilung.
Das Quantil können wir entweder grafisch oder rechnerisch bestimmen.
Das Konfidenzniveau beträgt in unserem Fall 99%. Für die grafische Variante zeichnen wir uns kurz eine Glockenkurve auf und die 99% zeichnen wir als symmetrischen Bereich ein.
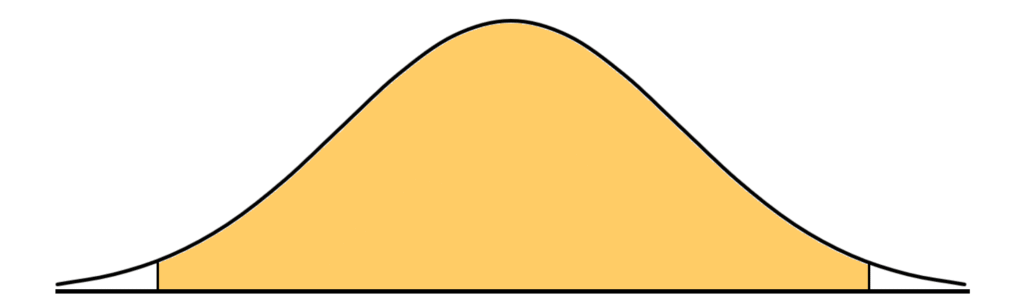
Wir sehen nun, dass links und rechts von diesem Bereich jeweils 0.5% der Dichte liegen. Wir suchen also den Wert, bei dem der orangene Bereich vom rechten weißen Bereiche getrennt wird. Links von diesem Wert liegen die 99% der Dichte (=orangener Bereich) und die 0,5% der Dichte im linken weißen Bereich. Insgesamt ergibt das 99.5% und das heißt wir suchen das 99.5% Quantil der T-Verteilung mit 19 Freiheitsgraden oder kurz ausgedrückt \(t_{0.995;19}\)
Um das dieses Quantil zu finden, benötigen wir die Tabelle der T-Verteilung.
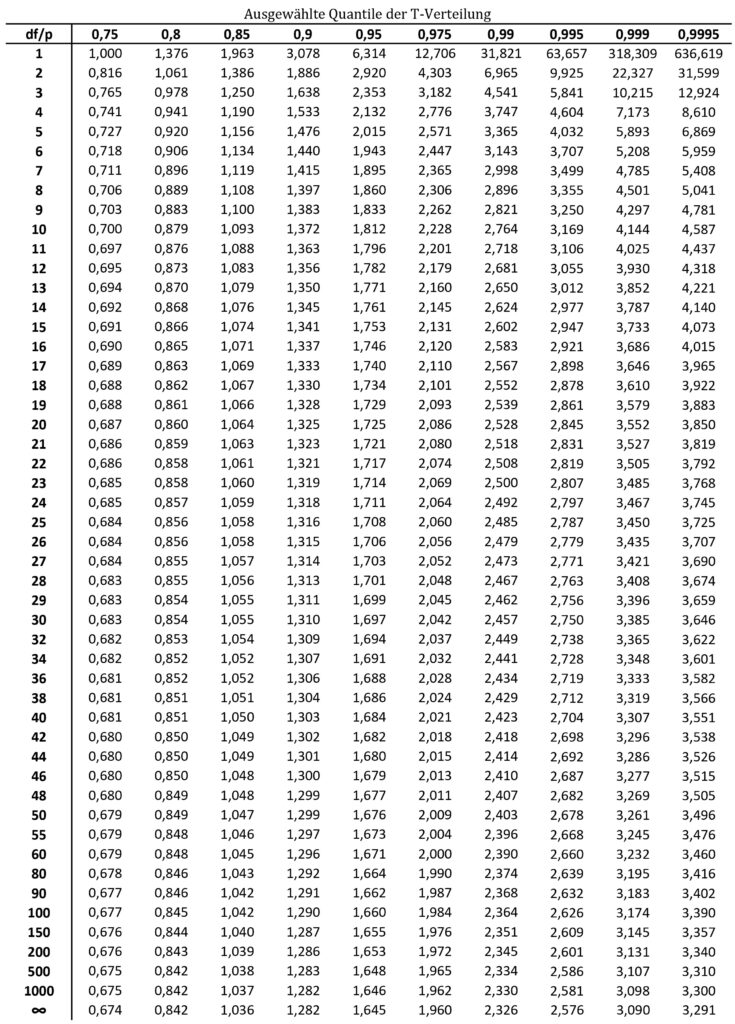
Wir suchen oben in den Spalten bei den Wahrscheinlichkeiten (p) den Wert von 0.995. Links in den Zeilen suchen wir in den Freiheitsgraden (df) den Wert 19. Der Schnittpunkt der entsprechenden Zeile und Spalte ergibt das gesuchte Quantil 2.861.
$$t_{0.995;19} = 2.861$$
Bitte beachtet, dass es unterschiedliche T-Tabellen gibt und eure eventuell ganz anders aussieht. Die Vorgehensweise zum Finden des richtigen Quantils kann bei euch also auch ganz anders sein.
Rechnerisch verwenden wir die Formel \(t_{1-\frac{\alpha}{2};df}\).
\(\alpha\) ist das Signifikanzniveau. Wenn wir ein Konfidenzniveau von 0.99 berechnen wollen, beträgt das Signifikanzniveau \(1-0.99 = 0.01\). Wir setzen also 0.01 für \(\alpha\) ein und wir wissen ja schon, dass wir 19 Freiheitsgrade haben.
$$t_{1-\frac{\alpha}{2};df} = t_{1-\frac{0.01}{2};19} = t_{1-0.005;19} = t_{0.995;19} = 2.861$$
Somit erhalten wir wie vorher t von 0,995 bei 19 Freiheitsgraden und schauen wieder in der Tabelle nach, um 2.861 zu erhalten.
Konfidenzintervall ermitteln
Da wir nun die gesamte Vorarbeit geleistet haben, können wir unsere Werte in das Konfidenzintervall einsetzten:
$$\begin{align}KI &= [\bar{x} \pm t_{1-\frac{\alpha}{2};df} \cdot \frac{s}{\sqrt{n}}]\\ KI &= [53.1 \pm 2.861 \cdot \frac{9.3}{\sqrt{20}}] \\ KI &= [53.1 \pm 2.861 \cdot 2.08] \\ KI &= [53.1 \pm 5.95] \\ KI &= [47.15; 59.05] \end{align}$$
Den Wert, den man erhält, indem man das Quantil mal dem Standardfehler multipliziert, nennt man die Schwankungsbreite (= 5.95). Die Länge des Konfidenzintervalls kann entweder bestimmt werden, indem man die Differenz von der oberen Intervallgrenze zur unteren Intervallgrenze berechnet oder man kann auch die Schwankungsbreite mal 2 rechnen.
$$\text{Länge des KI} = \text{obere Grenze} – \text{untere Grenze} = 59.05 – 47.15= 11.9$$
$$\text{Länge des KI} = 2 \cdot \text{Schwankungsbreite} = 2 \cdot t_{1-\frac{\alpha}{2};19} \cdot \frac{s}{\sqrt{n}} = 2 \cdot 5.95 = 11.9$$
Interpretation
Hier könnt ihr die Hilfestellungen verwenden, die ich euch im Einleitungsvideo zu Konfidenzintervallen bereitgestellt habe.
Mit so und so viel prozentiger Sicherheit, liegt der wahre Wert zwischen unterer und oberer Grenze.
Wir können mit der Hilfestellung sagen, dass mit 99-prozentiger Sicherheit der wahre Erwartungswert der durchschnittlichen Kundenausgaben zwischen 47.15€ und 59.05€ liegt.
Es gibt natürlich mehrere Möglichkeiten zur Formulierung der Interpretation.
T- vs. Z-Quantil
Nehmen wir dasselbe Beispiel von voher, aber sagen wir, dass wir 45 Personen befragt haben. Jetzt haben wir 44 Freiheitsgrade und nun ist die Frage, ob wir die T- oder die Normalverteilungstabelle zu Rate ziehen.
Nach unserer besprochenen Orientierungshilfe können wir hier das Quantil der Normalverteilung benutzen, da 44 größer als 30 ist.
Berechnen wir also das t- und z-Quantil und vergleichen die beiden:
$$t_{0.995;44} = 2.962$$
$$\begin{align} KI_1 &= [\bar{x} \pm t_{1-\frac{\alpha}{2};44} \cdot \frac{s}{\sqrt{n}}]\\ KI_1 &= [53.1 \pm 2.962 \cdot \frac{9.3}{\sqrt{45}}]\\ KI_1 &= [53.1 \pm 3.73] \\ KI_1 &= [49.37; 56.83] \end{align}$$
$$\text{Länge}_1 =7.46$$
$$z_{0.995} = 2.576$$
$$\begin{align} KI_2 &= [\bar{x} \pm z_{1-\frac{\alpha}{2}} \cdot \frac{s}{\sqrt{n}}]\\ KI_2 &= [53.1 \pm 2.576 \cdot \frac{9.3}{\sqrt{45}}]\\ KI_2 &= [53.1 \pm 3.57] \\ KI_2 &= [49.53; 56.67] \end{align}$$
$$\text{Länge}_2 =7.14$$
Das Konfidenzintervall der T-Verteilung ist somit etwas breiter als das der Normalverteilung. Wir sehen aber auch, dass der Unterschied zwischen den beiden Intervallen nicht allzu groß ist. Wie vorher schon erwähnt: Haltet euch an die Vorgaben eurer Schule bzw. Uni und wenn ihr euch unsicher seid, nehmt die Normalverteilungstabelle, sobald die Freiheitsgrade über die eure T-Tabelle hinausgehen.
Konfidenzintervall für Erwartungswert
In diesem Beitrag besprechen wir die Berechnung von Konfidenzintervallen für den Erwartungswert bei einer Stichprobe.
- Punktschätzer und Quantil bestimmen
- T-Verteilung bzw. Normalverteilung
- Konfidenzintervall berechnen
- Interpretation
Die Grundlagen zu Konfidenzintervallen werden im Beitrag Konfidenzintervalle – Erklärung genauer beschrieben. Das Wissen in diesem Beitrag wird hier vorausgesetzt.
Was ist ein Konfidenzintervall?
Ein Konfidenzintervall, auch Vertrauensintervall genannt, ist eine Schätzung für einen unbekannten Parameter. Es gibt einen Bereich an, in dem sich dieser unbekannte Parameter mit einer gewissen Sicherheit befinden soll. Konfidenzintervalle, auch wenn sie teilweise sehr unterschiedlich aussehen, sind im Allgemeinen gleich aufgebaut:
[Punktschätzer ± Quantil * Standardfehler]
Ein Konfidenzintervall für den Erwartungswert schaut so aus:
$$ [{\color{#2dacb4}{\bar{x}} \pm \color{#fc7a7a}{t_{1-\frac{\alpha}{2};df}}*\color{
#3094d4}{\frac{s}{\sqrt{n}}}} ]$$
Beim Konfidenzintervall für den Erwartungswert ist der Punktschätzer einfach der Mittelwert der Stichprobe. \(\bar{x}\).
Für das Quantil verwenden wir in der Regel die T-Verteilung und den Standardfehler erhalten wir, indem wir die Standardabweichung durch die Wurzel von n dividieren.
Hier ist wichtig, dass ihr die geschätzte Populationsstandardabweichung verwendet. Bei dieser wird durch n-1 anstatt durch n dividiert. Sie wird auch häufig mit \(\widehat{\sigma}\) abgekürzt.
Quantil bestimmen
Um dieses Konfidenzintervall bestimmen zu können, muss die Grundgesamtheit normalverteilt sein. Für die Berechnung ist wichtig, ob die Varianz der Population bekannt ist oder nicht.
Bei unbekannter Varianz verwenden wir in der Regel das Quantil der T-Verteilung.
Die T-Verteilung nähert sich mit wachsender Anzahl der Freiheitsgrade an die Standardnormalverteilung an.
Daher kann die T-Verteilung auch durch die Normalverteilung approximiert werden, wenn die Anzahl an Freiheitsgraden groß genug ist und wir können dann das Quantil der Standardnormalverteilung verwenden.
Welche Anzahl an Freiheitsgraden „groß genug“ ist, ist je nach Quelle unterschiedlich. Meistens wird der Wert 30 genannt. Das heißt also, wenn die Freiheitsgrade kleiner gleich 30 sind, verwenden wir das Quantil der T-Verteilung in unserem Konfidenzintervall.
$$df \leq 30: \quad [\bar{x} \pm t_{1-\frac{\alpha}{2};df} \cdot \frac{s}{\sqrt{n}}]$$
Wenn die Freiheitsgrade über 30 liegen, nehmen wir das Quantil der Standardnormalverteilung.
$$df \geq 30: \quad [\bar{x} \pm z_{1-\frac{\alpha}{2}} \cdot \frac{s}{\sqrt{n}}]$$
Auf Englisch heißen Freiheitsgrade übrigens degrees of freedom weswegen wir sie mit df abkürzen. Bitte beachtet, dass es nur eine grobe Orientierung ist, zu sagen, die Approximation der T-Verteilung durch die Normalverteilung wäre ab 30 Freiheitsgraden gut genug. Es gibt auch Quellen, die eine Annäherung erst ab 50 bzw. 100 Freiheitsgraden als ausreichend gut sehen.
Wann ihr die T- oder die Normalverteilungstabelle nehmt, kommt also darauf an, ab wann ihr Approximation der T-Verteilung durch die Normalverteilung für gut genug haltet. Am einfachsten ist, ihr verwendet die Tabelle zur T-Verteilung, die ihr von eurer Schule oder Uni bekommen habt und sobald die gegebenen Freiheitsgrade die Freiheitsgrade in eurer Tabelle überschreiten, verwendet ihr das Quantil der Normalverteilung.
Wenn die Varianz der Grundgesamtheit bekannt ist, dann verwenden wir das Quantil der Standardnormalverteilung und im Standardfehler dividieren wir nun die Populationsstandardabweichung durch den Stichprobenumfang.
$$\text{Varianz bekannt: } \quad [\bar{x} \pm z_{1-\frac{\alpha}{2}} \cdot \frac{\sigma}{n}]$$
Wie ihr aus dem Beitrag Konfidenzintervalle – Erklärung schon wisst, verwenden wir für Populationsparameter griechische Buchstaben – deswegen \(\sigma\).
In diesem Video werden wir nur auf den Fall der unbekannten Varianz eingehen.
Beispiel zur Berechnung
Für die Berechnung gehen wir davon aus, dass wir eine Firma haben und die durchschnittlichen Ausgaben unserer Kunden bestimmen wollen. Dafür haben wir eine Stichprobe von 20 Personen gezogen, wobei die mittleren Ausgaben dieser bei 53.1€ und die Standardabweichung bei 9.3€ liegen. Wir können davon ausgehen, dass die Ausgaben in der Grundgesamtheit normalverteilt sind und wir wollen nun das 99% Konfidenzintervall für den unbekannten Erwartungswert bestimmen.
$$\bar{x} = 53.1 \quad s = 9.3 \quad n = 20$$
Die Varianz der Grundgesamtheit ist also nicht bekannt. (Nur die Varianz der Stichprobe)
Wir haben zuvor schon erwähnt, dass die Wahl des Quantils von der Anzahl der Freiheitsgrade abhängt. In diesem Fall liegen uns n-1 Freiheitsgrade vor.
$$df = n-1 = 20 -1 = 19$$
Da wir 19 Freiheitsgrade haben, verwenden wir das Quantil der T-Verteilung.
Das Quantil können wir entweder grafisch oder rechnerisch bestimmen.
Das Konfidenzniveau beträgt in unserem Fall 99%. Für die grafische Variante zeichnen wir uns kurz eine Glockenkurve auf und die 99% zeichnen wir als symmetrischen Bereich ein.

Wir sehen nun, dass links und rechts von diesem Bereich jeweils 0.5% der Dichte liegen. Wir suchen also den Wert, bei dem der orangene Bereich vom rechten weißen Bereiche getrennt wird. Links von diesem Wert liegen die 99% der Dichte (=orangener Bereich) und die 0,5% der Dichte im linken weißen Bereich. Insgesamt ergibt das 99.5% und das heißt wir suchen das 99.5% Quantil der T-Verteilung mit 19 Freiheitsgraden oder kurz ausgedrückt \(t_{0.995;19}\)
Um das dieses Quantil zu finden, benötigen wir die Tabelle der T-Verteilung.

Wir suchen oben in den Spalten bei den Wahrscheinlichkeiten (p) den Wert von 0.995. Links in den Zeilen suchen wir in den Freiheitsgraden (df) den Wert 19. Der Schnittpunkt der entsprechenden Zeile und Spalte ergibt das gesuchte Quantil 2.861.
$$t_{0.995;19} = 2.861$$
Bitte beachtet, dass es unterschiedliche T-Tabellen gibt und eure eventuell ganz anders aussieht. Die Vorgehensweise zum Finden des richtigen Quantils kann bei euch also auch ganz anders sein.
Rechnerisch verwenden wir die Formel \(t_{1-\frac{\alpha}{2};df}\).
\(\alpha\) ist das Signifikanzniveau. Wenn wir ein Konfidenzniveau von 0.99 berechnen wollen, beträgt das Signifikanzniveau \(1-0.99 = 0.01\). Wir setzen also 0.01 für \(\alpha\) ein und wir wissen ja schon, dass wir 19 Freiheitsgrade haben.
$$t_{1-\frac{\alpha}{2};df} = t_{1-\frac{0.01}{2};19} = t_{1-0.005;19} = t_{0.995;19} = 2.861$$
Somit erhalten wir wie vorher t von 0,995 bei 19 Freiheitsgraden und schauen wieder in der Tabelle nach, um 2.861 zu erhalten.
Konfidenzintervall ermitteln
Da wir nun die gesamte Vorarbeit geleistet haben, können wir unsere Werte in das Konfidenzintervall einsetzten:
$$\begin{align}KI &= [\bar{x} \pm t_{1-\frac{\alpha}{2};df} \cdot \frac{s}{\sqrt{n}}]\\ KI &= [53.1 \pm 2.861 \cdot \frac{9.3}{\sqrt{20}}] \\ KI &= [53.1 \pm 2.861 \cdot 2.08] \\ KI &= [53.1 \pm 5.95] \\ KI &= [47.15; 59.05] \end{align}$$
Den Wert, den man erhält, indem man das Quantil mal dem Standardfehler multipliziert, nennt man die Schwankungsbreite (= 5.95). Die Länge des Konfidenzintervalls kann entweder bestimmt werden, indem man die Differenz von der oberen Intervallgrenze zur unteren Intervallgrenze berechnet oder man kann auch die Schwankungsbreite mal 2 rechnen.
$$\text{Länge des KI} = \text{obere Grenze} – \text{untere Grenze} = 59.05 – 47.15= 11.9$$
$$\text{Länge des KI} = 2 \cdot \text{Schwankungsbreite} = 2 \cdot t_{1-\frac{\alpha}{2};19} \cdot \frac{s}{\sqrt{n}} = 2 \cdot 5.95 = 11.9$$
Interpretation
Hier könnt ihr die Hilfestellungen verwenden, die ich euch im Einleitungsvideo zu Konfidenzintervallen bereitgestellt habe.
Mit so und so viel prozentiger Sicherheit, liegt der wahre Wert zwischen unterer und oberer Grenze.
Wir können mit der Hilfestellung sagen, dass mit 99-prozentiger Sicherheit der wahre Erwartungswert der durchschnittlichen Kundenausgaben zwischen 47.15€ und 59.05€ liegt.
Es gibt natürlich mehrere Möglichkeiten zur Formulierung der Interpretation.
T- vs. Z-Quantil
Nehmen wir dasselbe Beispiel von voher, aber sagen wir, dass wir 45 Personen befragt haben. Jetzt haben wir 44 Freiheitsgrade und nun ist die Frage, ob wir die T- oder die Normalverteilungstabelle zu Rate ziehen.
Nach unserer besprochenen Orientierungshilfe können wir hier das Quantil der Normalverteilung benutzen, da 44 größer als 30 ist.
Berechnen wir also das t- und z-Quantil und vergleichen die beiden:
$$t_{0.995;44} = 2.962$$
$$\begin{align} KI_1 &= [\bar{x} \pm t_{1-\frac{\alpha}{2};44} \cdot \frac{s}{\sqrt{n}}]\\ KI_1 &= [53.1 \pm 2.962 \cdot \frac{9.3}{\sqrt{45}}]\\ KI_1 &= [53.1 \pm 3.73] \\ KI_1 &= [49.37; 56.83] \end{align}$$
$$\text{Länge}_1 =7.46$$
$$z_{0.995} = 2.576$$
$$\begin{align} KI_2 &= [\bar{x} \pm z_{1-\frac{\alpha}{2}} \cdot \frac{s}{\sqrt{n}}]\\ KI_2 &= [53.1 \pm 2.576 \cdot \frac{9.3}{\sqrt{45}}]\\ KI_2 &= [53.1 \pm 3.57] \\ KI_2 &= [49.53; 56.67] \end{align}$$
$$\text{Länge}_2 =7.14$$
Das Konfidenzintervall der T-Verteilung ist somit etwas breiter als das der Normalverteilung. Wir sehen aber auch, dass der Unterschied zwischen den beiden Intervallen nicht allzu groß ist. Wie vorher schon erwähnt: Haltet euch an die Vorgaben eurer Schule bzw. Uni und wenn ihr euch unsicher seid, nehmt die Normalverteilungstabelle, sobald die Freiheitsgrade über die eure T-Tabelle hinausgehen.
