Tauche ein in unsere modebewusste Statistik-Welt.
Disjunkte Ereignisse
Dieser Beitrag beschäftigt sich mit den wichtigsten disjunkten Ereignissen und soll die folgenden Fragen beantworten:
- Was sind disjunkte Ereignissen?
- Wie berechne ich die Wahrscheinlichkeit bei disjunkten Ereignissen?
- Wie stelle ich disjunkte Ereignisse als Venn Diagramm dar?
Definition
Disjunkte Ereignisse sind Ereignisse eines Zufallsexperiments, die sich gegenseitig ausschließen. Mit anderen Worten sind zwei Ereignisse \(A\) und \(B\) disjunkt, wenn sie sich nicht überschneiden, also wenn die Schnittmenge der beiden Ereignisse der leeren Menge entspricht: $$A \cap B = \emptyset.$$
Beispiel
Bezugnehmend auf das Beispiel des Würfelns sind zum Beispiel die Ereignisse „Augenzahl ist gerade“ und „Augenzahl ist ungerade“ disjunkt, da sie einander selbstverständlich ausschließen. Und tatsächlich gilt, formal geschrieben, $$\{2,4,6\} \cap \{1,3,5\} = \emptyset.$$
Wie ihr im Beitrag zu den Axiomen von Kolmogorov nachlesen könnt, besagt die Additivität, dass für zwei disjunkte Ereignisse \(A\) und \(B\) gelten muss, dass: $$P(A \cup B ) = P(A) + P(B)$$
Wenn disjunkte Ereignisse mittels eines Venn-Diagramms dargestellt werden, kann das folgendermaßen aussehen:
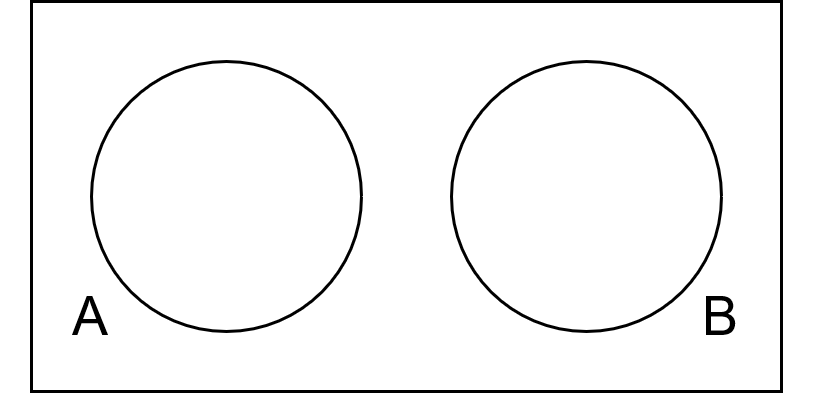
Falls die beiden Ereignisse NICHT den gesamten Ereignisraum einnehmen.
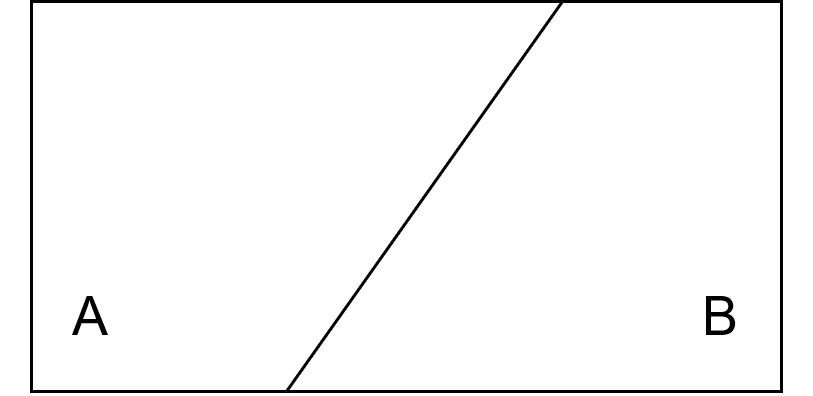
Falls die beiden Ereignisse den gesamten Ereignisraum einnehmen.
Wollt ihr mehr zu den Grundlagen der Wahrscheinlichkeitsrechnung erfahren, seht euch das folgende Video zu den Axiomen von Kolmogorov an:

Disjunkte Ereignisse
Dieser Beitrag beschäftigt sich mit den wichtigsten disjunkten Ereignissen und soll die folgenden Fragen beantworten:
- Was sind disjunkte Ereignissen?
- Wie berechne ich die Wahrscheinlichkeit bei disjunkten Ereignissen?
- Wie stelle ich disjunkte Ereignisse als Venn Diagramm dar?
Definition
Disjunkte Ereignisse sind Ereignisse eines Zufallsexperiments, die sich gegenseitig ausschließen. Mit anderen Worten sind zwei Ereignisse \(A\) und \(B\) disjunkt, wenn sie sich nicht überschneiden, also wenn die Schnittmenge der beiden Ereignisse der leeren Menge entspricht: $$A \cap B = \emptyset.$$
Beispiel
Bezugnehmend auf das Beispiel des Würfelns sind zum Beispiel die Ereignisse „Augenzahl ist gerade“ und „Augenzahl ist ungerade“ disjunkt, da sie einander selbstverständlich ausschließen. Und tatsächlich gilt, formal geschrieben, $$\{2,4,6\} \cap \{1,3,5\} = \emptyset.$$
Wie ihr im Beitrag zu den Axiomen von Kolmogorov nachlesen könnt, besagt die Additivität, dass für zwei disjunkte Ereignisse \(A\) und \(B\) gelten muss, dass: $$P(A \cup B ) = P(A) + P(B)$$
Wenn disjunkte Ereignisse mittels eines Venn-Diagramms dargestellt werden, kann das folgendermaßen aussehen:

Falls die beiden Ereignisse NICHT den gesamten Ereignisraum einnehmen.

Falls die beiden Ereignisse den gesamten Ereignisraum einnehmen.
Wollt ihr mehr zu den Grundlagen der Wahrscheinlichkeitsrechnung erfahren, seht euch das folgende Video zu den Axiomen von Kolmogorov an:

