Tauche ein in unsere modebewusste Statistik-Welt.
Schiefe – Berechnung
Heute geht es um die Schiefe.
- Berechnung der Schiefe
- Quartilsschiefe
- Momentschiefe
Wichtiges Vorwissen zu diesem Beitrag ist die Erklärung zur Schiefe sowie die Lagemaße.
Außerdem ist es hilfreich, wenn ihr auch schon wisst was Boxplots sind und wie man die Standardabweichung berechnet.
Quartilsschiefe
Wie wir zuvor schon gesehen haben, kann man die Schiefe auch gut anhand von Boxplots erkennen. Zudem wissen wir, dass Boxplots die Quartile zeigen, also das 25% (Q1), 50% (Q2) und 75% Quantil (Q3).
Vielleicht habt ihr schon erkannt, dass bei einer rechtsschiefen Verteilung so wie es hier der Fall ist, Q1 und Q2 näher beisammen liegen als Q2 und Q3.
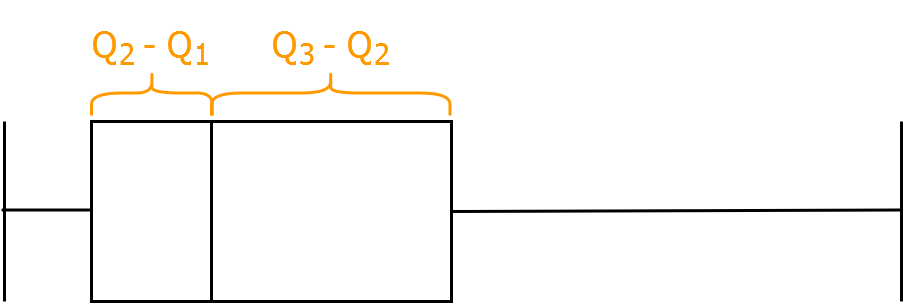
Das bedeutet also, wenn die Differenz von Q3 zu Q2 größer ist als von Q2 zu Q1 dann handelt es sich um eine rechtsschiefe Verteilung.
Falls umgekehrt (die Differenz von Q2 zu Q1 größer ist als von Q3 zu Q2), handelt es sich um eine linksschiefe Verteilung. Aus dieser Idee heraus können wir die Formel für die Quartilsschiefe herleiten.
Also der Abstand zwischen Q3 und Q2 (Q3 – Q2) – dem Abstand zwischen Q2 und Q1 (Q2 – Q1) und das Ganze noch geteilt durch den Interquartilsabstand, also durch (Q3 – Q1).
$$
S_q = \frac{(Q3 – Q2) – (Q2 – Q1)}{(Q3 – Q1)}
$$
Als Beispiel nehmen wir kurz an, dass wir die Schiefe einer Einkommensverteilung untersuchen wollen, wobei das 1. Quartil bei 1200, das Zweite, also der Median bei 1500 und das Dritte bei 2500 Euro liegt. Diese drei Werte müssen wir nur in die Formel einsetzen und erhalten somit einen Wert von 0.54.
Da der Wert positiv ist, wissen wir also dass die Verteilung rechtsschief sein muss. Die Quartilsschiefe kann dabei nur Werte zwischen -1 und 1 annehmen.
$$\begin{aligned}Q1 = 1200\\Q2 = 1500\\Q3 = 2500\end{aligned}$$
$$\begin{align*}S_q &= \frac{(2500 – 1500) – (1500 – 1200)}{(2500 – 1200)}\\S_q &= \frac{1000 -300}{1300}\\S_q &= 0.54\end{align*}$$
Momentschiefe
Die Momentschiefe ist die aufwendigste Berechnungsform der Schiefe. Sie ist das normierte dritte Moment und die Formel schaut so aus:
$$ \nu = \frac{1}{n}\sum_{i=1}^{n}\left(\frac{x_i – \bar{x}}{s}\right)^3$$
Man kann die Berechnung etwas vereinfachen, indem wir die Formel umstellen.
$$ \nu = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i – \bar{x})^3}{s^3}$$
Beispiel
Als Beispiel nehmen wir dieses Mal die Ankunftszeiten ein paar ausgewählter Läufer bei einem Halbmarathon. Die Zeiten sind in Minuten angegeben, wobei die schnellste Person eine Stunde und die langsamste 3 Stunden benötigte.
$$ 60,65,80,85,125,155,160,165,175,180$$
Zur Berechnung der Schiefe benötigen wir die Standardabweichung. In diesem Fall nehmen wir die Formel der Quadrierten Abweichungen, da wir die Abweichungen ohnehin auch für die Berechnung der Schiefe benötigen. Ansonsten verwendet bitte immer die rechentechnisch günstigere Formel. Wenn ihr nicht wisst, wovon ich spreche, seht euch bitte den Beitrag zur Standardabweichung und Varianz nochmals an.
$$s^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i – \bar{x})^2$$
Zur Berechnung benötigen wir also die Abweichungen zum Mittelwert, die quadrierten Abweichungen sowie die Abweichungen zur dritten Potenz. Außerdem brauchen wir noch den Mittelwert.
Wir berechnen zuerst den Mittelwert. Einfach alles zusammenzählen und durch die Anzahl der Datenpunkte (n = 10) dividieren und wir erhalten 125 als Durchschnitt. Auch gut zu sehen in der gleich folgenden Tabelle
$$ \bar{x} = 125 $$
Als erste Spalte in unserer Tabelle rechnen wir nun jeden x Wert minus dem Mittelwert. Im ersten Fall also \(60 – 125 = -65 \).
Dasselbe für die restlichen Werte und natürlich erhalten wir als Summe der Abweichungen wieder Null.
Als nächstes brauchen wir die quadrierten Abweichungen, also jede der Abweichungen hoch 2 rechnen. \((-65)^2 = 4225\).
Dasselbe wieder für den Rest und als Summe erhalten wir 20700.
Als letztes dasselbe Spiel noch für \((x_i – \bar{x})^3\). Wenn wir jede Abweichung hoch 3 zusammenrechnen erhalten wir als Summe -220.500.
| \(x_i\) | \((x_i-\bar{x})\) | \((x_i-\bar{x})^2\) | \((x_i-\bar{x})^3\) |
| 60 | -65 | 4225 | -274625 |
| 65 | -60 | 3600 | -216000 |
| 80 | -45 | 2025 | -91125 |
| 85 | -40 | 1600 | -64000 |
| 125 | 0 | 0 | 0 |
| 155 | 30 | 900 | 27000 |
| 160 | 35 | 1225 | 42875 |
| 165 | 40 | 1600 | 64000 |
| 175 | 50 | 2500 | 125000 |
| 180 | 55 | 3025 | 166375 |
| \(\boldsymbol{\sum 1250}\) | 0 | 20700 | –220500 |
Nun haben wir alle notwendigen Werte und können sie in die Formeln einsetzen.
Zuerst berechnen wir die Varianz, also Summe der quadrierten Abweichungen dividiert durch die Anzahl der Datenpunkte:
$$\begin{aligned}s^2 = \frac{2700}{10}\\s^2 = 270\end{aligned}$$
Um die Standardabweichung zu ermitteln, berechnen wir die Wurzel von der Varianz.
$$s=45.5$$
Nun berechnen wir noch die Schiefe mithilfe der vorgestellten Formel
$$\nu = \frac{\frac{1}{10}*(-220500)}{45.5^3} = -0.23$$
Wir bekommen für die Schiefe -0.23 womit es sich um eine linksschiefe Verteilung handelt.
Schiefe – Berechnung
Heute geht es um die Schiefe.
- Berechnung der Schiefe
- Quartilsschiefe
- Momentschiefe
Wichtiges Vorwissen zu diesem Beitrag ist die Erklärung zur Schiefe sowie die Lagemaße.
Außerdem ist es hilfreich, wenn ihr auch schon wisst was Boxplots sind und wie man die Standardabweichung berechnet.
Quartilsschiefe
Wie wir zuvor schon gesehen haben, kann man die Schiefe auch gut anhand von Boxplots erkennen. Zudem wissen wir, dass Boxplots die Quartile zeigen, also das 25% (Q1), 50% (Q2) und 75% Quantil (Q3).
Vielleicht habt ihr schon erkannt, dass bei einer rechtsschiefen Verteilung so wie es hier der Fall ist, Q1 und Q2 näher beisammen liegen als Q2 und Q3.

Das bedeutet also, wenn die Differenz von Q3 zu Q2 größer ist als von Q2 zu Q1 dann handelt es sich um eine rechtsschiefe Verteilung.
Falls umgekehrt (die Differenz von Q2 zu Q1 größer ist als von Q3 zu Q2), handelt es sich um eine linksschiefe Verteilung. Aus dieser Idee heraus können wir die Formel für die Quartilsschiefe herleiten.
Also der Abstand zwischen Q3 und Q2 (Q3 – Q2) – dem Abstand zwischen Q2 und Q1 (Q2 – Q1) und das Ganze noch geteilt durch den Interquartilsabstand, also durch (Q3 – Q1).
$$
S_q = \frac{(Q3 – Q2) – (Q2 – Q1)}{(Q3 – Q1)}
$$
Als Beispiel nehmen wir kurz an, dass wir die Schiefe einer Einkommensverteilung untersuchen wollen, wobei das 1. Quartil bei 1200, das Zweite, also der Median bei 1500 und das Dritte bei 2500 Euro liegt. Diese drei Werte müssen wir nur in die Formel einsetzen und erhalten somit einen Wert von 0.54.
Da der Wert positiv ist, wissen wir also dass die Verteilung rechtsschief sein muss. Die Quartilsschiefe kann dabei nur Werte zwischen -1 und 1 annehmen.
$$\begin{aligned}Q1 = 1200\\Q2 = 1500\\Q3 = 2500\end{aligned}$$
$$\begin{align*}S_q &= \frac{(2500 – 1500) – (1500 – 1200)}{(2500 – 1200)}\\S_q &= \frac{1000 -300}{1300}\\S_q &= 0.54\end{align*}$$
Momentschiefe
Die Momentschiefe ist die aufwendigste Berechnungsform der Schiefe. Sie ist das normierte dritte Moment und die Formel schaut so aus:
$$ \nu = \frac{1}{n}\sum_{i=1}^{n}\left(\frac{x_i – \bar{x}}{s}\right)^3$$
Man kann die Berechnung etwas vereinfachen, indem wir die Formel umstellen.
$$ \nu = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i – \bar{x})^3}{s^3}$$
Beispiel
Als Beispiel nehmen wir dieses Mal die Ankunftszeiten ein paar ausgewählter Läufer bei einem Halbmarathon. Die Zeiten sind in Minuten angegeben, wobei die schnellste Person eine Stunde und die langsamste 3 Stunden benötigte.
$$ 60,65,80,85,125,155,160,165,175,180$$
Zur Berechnung der Schiefe benötigen wir die Standardabweichung. In diesem Fall nehmen wir die Formel der Quadrierten Abweichungen, da wir die Abweichungen ohnehin auch für die Berechnung der Schiefe benötigen. Ansonsten verwendet bitte immer die rechentechnisch günstigere Formel. Wenn ihr nicht wisst, wovon ich spreche, seht euch bitte den Beitrag zur Standardabweichung und Varianz nochmals an.
$$s^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i – \bar{x})^2$$
Zur Berechnung benötigen wir also die Abweichungen zum Mittelwert, die quadrierten Abweichungen sowie die Abweichungen zur dritten Potenz. Außerdem brauchen wir noch den Mittelwert.
Wir berechnen zuerst den Mittelwert. Einfach alles zusammenzählen und durch die Anzahl der Datenpunkte (n = 10) dividieren und wir erhalten 125 als Durchschnitt. Auch gut zu sehen in der gleich folgenden Tabelle
$$ \bar{x} = 125 $$
Als erste Spalte in unserer Tabelle rechnen wir nun jeden x Wert minus dem Mittelwert. Im ersten Fall also \(60 – 125 = -65 \).
Dasselbe für die restlichen Werte und natürlich erhalten wir als Summe der Abweichungen wieder Null.
Als nächstes brauchen wir die quadrierten Abweichungen, also jede der Abweichungen hoch 2 rechnen. \((-65)^2 = 4225\).
Dasselbe wieder für den Rest und als Summe erhalten wir 20700.
Als letztes dasselbe Spiel noch für \((x_i – \bar{x})^3\). Wenn wir jede Abweichung hoch 3 zusammenrechnen erhalten wir als Summe -220.500.
| \(x_i\) | \((x_i-\bar{x})\) | \((x_i-\bar{x})^2\) | \((x_i-\bar{x})^3\) |
| 60 | -65 | 4225 | -274625 |
| 65 | -60 | 3600 | -216000 |
| 80 | -45 | 2025 | -91125 |
| 85 | -40 | 1600 | -64000 |
| 125 | 0 | 0 | 0 |
| 155 | 30 | 900 | 27000 |
| 160 | 35 | 1225 | 42875 |
| 165 | 40 | 1600 | 64000 |
| 175 | 50 | 2500 | 125000 |
| 180 | 55 | 3025 | 166375 |
| \(\boldsymbol{\sum 1250}\) | 0 | 20700 | –220500 |
Nun haben wir alle notwendigen Werte und können sie in die Formeln einsetzen.
Zuerst berechnen wir die Varianz, also Summe der quadrierten Abweichungen dividiert durch die Anzahl der Datenpunkte:
$$\begin{aligned}s^2 = \frac{2700}{10}\\s^2 = 270\end{aligned}$$
Um die Standardabweichung zu ermitteln, berechnen wir die Wurzel von der Varianz.
$$s=45.5$$
Nun berechnen wir noch die Schiefe mithilfe der vorgestellten Formel
$$\nu = \frac{\frac{1}{10}*(-220500)}{45.5^3} = -0.23$$
Wir bekommen für die Schiefe -0.23 womit es sich um eine linksschiefe Verteilung handelt.
