Tauche ein in unsere modebewusste Statistik-Welt.
Konfidenzintervall für einen Anteil
- Punktschätzer und Quantil bestimmen
- Konfidenzintervall berechnen
- Interpretation
Die Grundlagen zu Konfidenzintervallen werden im Beitrag Konfidenzintervalle – Erklärung genauer beschrieben. Das Wissen in diesem Beitrag wird hier vorausgesetzt.
Was ist ein Konfidenzintervall?
Ein Konfidenzintervall, auch Vertrauensintervall genannt, ist eine Schätzung für einen unbekannten Parameter. Es gibt einen Bereich an, in dem sich dieser unbekannte Parameter mit einer gewissen Sicherheit befinden soll. Konfidenzintervalle, auch wenn sie teilweise sehr unterschiedlich aussehen, sind im Allgemeinen gleich aufgebaut:
[Punktschätzer ± Quantil * Standardfehler]
Ein Konfidenzintervall für einen Anteil schaut so aus:
$$ {\color{#2dacb4}{\widehat{p}} \pm \color{#fc7a7a}{z_{1-\frac{\alpha}{2}}}*\color{
#3094d4}{\sqrt{\frac{\widehat{p}-(1-\widehat{p})}{n}}}} $$
Im Beitrag Konfidenzintervalle – Erklärung haben wir uns ein Beispiel zur Bestimmung des Wähleranteils einer Partei angeschaut. Nun wird gezeigt, wie man das entsprechende Konfidenzintervall berechnet.
Berechnung
Es ging darum, den wahren Wähleranteil einer Partei zu schätzen. Dazu haben wir 500 Personen befragt und 150 davon haben gesagt, dass sie die Partei zum aktuellen Zeitpunkt wählen würden. Das Konfidenzniveau soll eine Sicherheit von 95% haben.
Wir bezeichnen mit X die Anzahl der Wähler der Partei in der Stichprobe.
Den Stichprobenumfang n haben wir schon gegeben, dieser beträgt 500.
Den Punktschätzer p-Dach \(\widehat{p}\) stellt den Anteil der Wähler der Partei dar. Wir erhalten ihn, indem wir X durch n dividieren. 150 Personen haben gesagt, sie würden die Partei wählen, also rechnen wir 150 durch 500, was 0.3 ergibt.
$$\begin{align}X &= 150 \\ n &= 500\end{align}$$
$$\begin{align}\widehat{p} &= \frac{X}{n} \\ \widehat{p} &= \frac{150}{500} \\ \widehat{p}&=0.3\end{align}$$
Quantil graphisch bestimmen
Jetzt fehlt uns nur noch das \(1-\frac{\alpha}{2}\)-Quantil zu bestimmen. Dafür habt ihr 2 Möglichkeiten. Ihr könnt dies graphisch oder rechnerisch machen.
Das Konfidenzniveau hat in unserem Fall ein gewähltes Signifikanzniveau von 95% (dh. \(1 -\alpha = 0.95\)).
Für die grafische Methode zeichnen wir uns kurz die Glockenkurve der Standardnormalverteilung auf und dann zeichnen wir die 95% als symmetrischen Bereich ein.
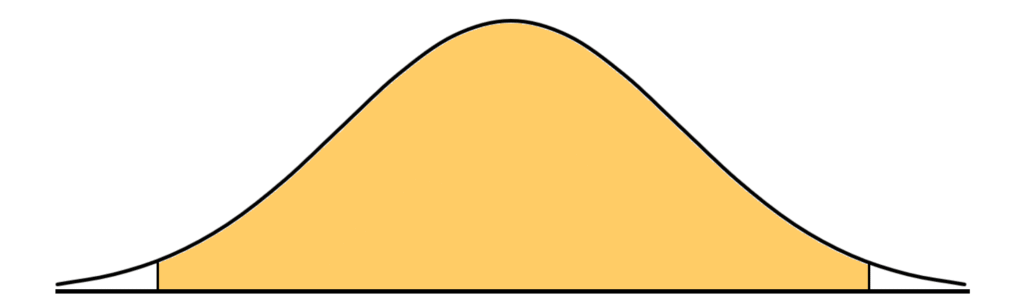
Wir sehen nun, dass links und rechts von diesem Bereich jeweils 2.5% der Dichte liegen. Dieser Bereich ist hier weiß. Wir suchen nun dieses Quantil, das auf der Grenze des gelben und weißen Bereichs liegt. An diesem Quantil liegen die 95% und die linken 2.5% links von unserem Quantil und die rechten 2.5% rechts des Quantils. Insgesamt sind also 97.5% der Datenpunkte kleiner als das Quantil, was bedeutet, wir suchen das 97.5% Quantil der Verteilung oder anders ausgedrückt, z an der Stelle 0.975.
Um das entsprechende Quantil zu finden, benötigen wir die Tabelle der Standardnormalverteilung.
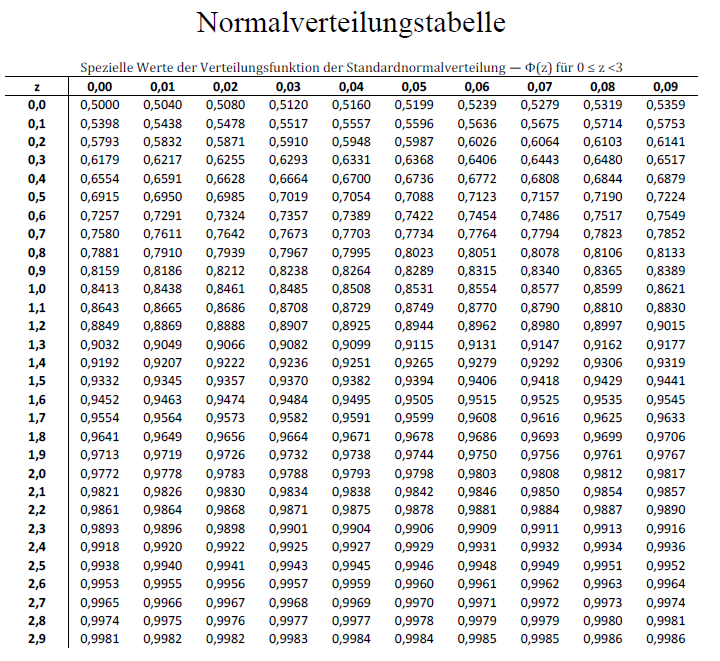
Wir suchen innerhalb der Tabelle bei den Wahrscheinlichkeiten den Wert von 0.975 bzw. wenn dieser nicht direkt in der Tabelle zu finden ist, den Wert der diesem am nächsten kommt.
Den Wert 0.975 finden wir in der 7. Spalte (unter 0.06) und der 20. Zeile (bei 1.9).
Den korrespondierenden z-Wert erhalten wir nun ganz einfach, indem wir die Werte in der entsprechenden Zeile und Spalte ablesen. In der Zeile haben wir 1.9 und in der Spalte 0.06. Der gesuchte z-Wert ist somit 1.96.
Bitte beachtet, dass es unterschiedliche Normalverteilungstabellen gibt und eure eventuell ganz anders aussieht. Die Vorgehensweise zum Finden des richtigen Quantils kann bei euch also auch ganz anders sein.
Details zur Normalverteilungstabelle
Um besser nachvollziehen zu können, was wir gerade ausgerechnet haben, hilft es sich zu erinnern, wie die Normalverteilung von oben aussieht:
In der Mitte auf der Höhe des Gipfels der Standardnormalverteilung befindet sich der Mittelwert, welcher 0 ist. Jetzt erkennt man leicht, was wir mit „symmetrischem Bereich“ gemeint haben, da die Verteilung symmetrisch ist. Der rechte Wert, bei dem der orange Bereich vom weißen Bereich getrennt wird, ist derselbe wie auf der linken Seite nur mit unterschiedlichem Vorzeichen. Daher hätten wir auch das Quantil berechnen können, bei dem 2.5% der Verteilung links und 97.5% rechts liegen. Das wäre das 2.5%-Quantil bzw. der z Wert an der Stelle 0.025. Ihr seht, dass dieser Wert auf der gegebenen Tabelle gar nicht drauf ist. Das ist der Fall, weil sie so konstruiert ist, dass sie nur positive z-Werte abbildet. Das 2.5%- Quantil hat nämlich denselben Wert, wie das 97.5%-Quantil nur negativ. Also -1.96. Daher reicht es, die Hälfte der z-Werte zu tabellieren und die passende Wahrscheinlichkeit zum Nachschlagen zu verwenden.
Quantil rechnerisch bestimmen
Rechnerisch sieht das Bestimmen des Quantils wie folgt aus. In unserer Formel steht \(z_{1-\frac{\alpha}{2}}\). \(\alpha\) ist ja bekanntlich das Signifikanzniveau. Wenn wir ein Konfidenzniveau von 0.95 gegeben haben, dann beträgt das Signifikanzniveau 0.05. Das heißt für \(\alpha\) setzen wir 0.05 ein.
$$z_{1-\frac{0.05}{2}} = z_{1-0.025} = z_{0.975} $$
Somit erhalten wir wie vorher den z-Wert von 0.975 und schauen diesen Wert erneut in der Tabelle nach, um 1.96 zu erhalten.
Ihr könnt also mit diesen beiden Methoden ganz einfach das korrekte Quantil herausfinden. In den meisten Fällen werden jedoch das 90, 95 und 99% Konfidenzintervall verwendet. Das heißt ihr könnt euch die folgenden Werte (auf 2 Nachkommastellen gerundet) auch einfach auswendig merken:
| Konfidenzintervall | z-Wert |
| 90% | 1.645 |
| 95% | 1.96 |
| 99% | 2.58 |
Konfidenzintervall bestimmen
Berechnen wir noch kurz den Standardfehler:
$$s = \sqrt{\frac{\widehat{p}-(1-\widehat{p})}{n}} = \sqrt{\frac{0.3-0.7}{500}} = 0.0205 $$
Jetzt haben wir alle Werte, die wir brauchen
$$\widehat{p} = 0.3 \quad z_{1-\frac{\alpha}{2}} = 1.96 \quad s = 0.0205$$
und wir können sie in die Formel einsetzen.
$$\begin{aligned} KI &= [\widehat{p} – z_{1-\frac{\alpha}{2}} \cdot s; \widehat{p} + z_{1-\frac{\alpha}{2}} \cdot s] \\ KI &= [0.3 – 1.96 \cdot 0.0205; 0.3 + 1.96 \cdot 0.0205] \\ KI &= [0.3 – 0.0402; 0.3 – 0.0402] \\ KI &= [0.2598; 0.3402]\end{aligned}$$
Wie im Erklärungsbeitrag schon erwähnt, stellt das Quantil * Standardfehler, also 0.0402 die Schwankungsbreite dar. Die Differenz von oberer zu unterer Grenze beschreibt die Länge des Intervalls.
Um die Länge zu erhalten, könnt ihr entweder besagte Differenz berechnen, oder noch einfacher ihr rechnet 2 Mal die Schwankungsbreite. Die Länge beträgt somit
$$\text{Länge des KI} = \text{obere Grenze} – \text{untere Grenze} = 0.3402 – 0.2598= 0.0804$$
$$\text{Länge des KI} = 2 \cdot \text{Schwankungsbreite} = 2 \cdot z_{1-\frac{\alpha}{2}} \cdot s = 2 \cdot 0.0402 = 0.0804$$
Interpretation
Hier könnt ihr die Hilfestellungen verwenden, die ich euch im Einleitungsvideo zu Konfidenzintervallen bereitgestellt habe.
Mit so und so viel prozentiger Sicherheit, liegt der wahre Wert zwischen unterer und oberer Grenze.
In diesem Fall heißt das also, dass der wahre Anteil der Wahlberechtigten, die für unsere Partei stimmen mit 95-prozentiger Sicherheit zwischen 25.98 und 34.02 Prozent liegt.
Es gibt natürlich mehrere Möglichkeiten die Interpretation zu formulieren, mehr dazu findet ihr im Erklärungsbeitrag zu Konfidenzintervallen.
Konfidenzintervall für einen Anteil
- Punktschätzer und Quantil bestimmen
- Konfidenzintervall berechnen
- Interpretation
Die Grundlagen zu Konfidenzintervallen werden im Beitrag Konfidenzintervalle – Erklärung genauer beschrieben. Das Wissen in diesem Beitrag wird hier vorausgesetzt.
Was ist ein Konfidenzintervall?
Ein Konfidenzintervall, auch Vertrauensintervall genannt, ist eine Schätzung für einen unbekannten Parameter. Es gibt einen Bereich an, in dem sich dieser unbekannte Parameter mit einer gewissen Sicherheit befinden soll. Konfidenzintervalle, auch wenn sie teilweise sehr unterschiedlich aussehen, sind im Allgemeinen gleich aufgebaut:
[Punktschätzer ± Quantil * Standardfehler]
Ein Konfidenzintervall für einen Anteil schaut so aus:
$$ {\color{#2dacb4}{\widehat{p}} \pm \color{#fc7a7a}{z_{1-\frac{\alpha}{2}}}*\color{
#3094d4}{\sqrt{\frac{\widehat{p}-(1-\widehat{p})}{n}}}} $$
Im Beitrag Konfidenzintervalle – Erklärung haben wir uns ein Beispiel zur Bestimmung des Wähleranteils einer Partei angeschaut. Nun wird gezeigt, wie man das entsprechende Konfidenzintervall berechnet.
Berechnung
Es ging darum, den wahren Wähleranteil einer Partei zu schätzen. Dazu haben wir 500 Personen befragt und 150 davon haben gesagt, dass sie die Partei zum aktuellen Zeitpunkt wählen würden. Das Konfidenzniveau soll eine Sicherheit von 95% haben.
Wir bezeichnen mit X die Anzahl der Wähler der Partei in der Stichprobe.
Den Stichprobenumfang n haben wir schon gegeben, dieser beträgt 500.
Den Punktschätzer p-Dach \(\widehat{p}\) stellt den Anteil der Wähler der Partei dar. Wir erhalten ihn, indem wir X durch n dividieren. 150 Personen haben gesagt, sie würden die Partei wählen, also rechnen wir 150 durch 500, was 0.3 ergibt.
$$\begin{align}X &= 150 \\ n &= 500\end{align}$$
$$\begin{align}\widehat{p} &= \frac{X}{n} \\ \widehat{p} &= \frac{150}{500} \\ \widehat{p}&=0.3\end{align}$$
Quantil graphisch bestimmen
Jetzt fehlt uns nur noch das \(1-\frac{\alpha}{2}\)-Quantil zu bestimmen. Dafür habt ihr 2 Möglichkeiten. Ihr könnt dies graphisch oder rechnerisch machen.
Das Konfidenzniveau hat in unserem Fall ein gewähltes Signifikanzniveau von 95% (dh. \(1 -\alpha = 0.95\)).
Für die grafische Methode zeichnen wir uns kurz die Glockenkurve der Standardnormalverteilung auf und dann zeichnen wir die 95% als symmetrischen Bereich ein.

Wir sehen nun, dass links und rechts von diesem Bereich jeweils 2.5% der Dichte liegen. Dieser Bereich ist hier weiß. Wir suchen nun dieses Quantil, das auf der Grenze des gelben und weißen Bereichs liegt. An diesem Quantil liegen die 95% und die linken 2.5% links von unserem Quantil und die rechten 2.5% rechts des Quantils. Insgesamt sind also 97.5% der Datenpunkte kleiner als das Quantil, was bedeutet, wir suchen das 97.5% Quantil der Verteilung oder anders ausgedrückt, z an der Stelle 0.975.
Um das entsprechende Quantil zu finden, benötigen wir die Tabelle der Standardnormalverteilung.

Wir suchen innerhalb der Tabelle bei den Wahrscheinlichkeiten den Wert von 0.975 bzw. wenn dieser nicht direkt in der Tabelle zu finden ist, den Wert der diesem am nächsten kommt.
Den Wert 0.975 finden wir in der 7. Spalte (unter 0.06) und der 20. Zeile (bei 1.9).
Den korrespondierenden z-Wert erhalten wir nun ganz einfach, indem wir die Werte in der entsprechenden Zeile und Spalte ablesen. In der Zeile haben wir 1.9 und in der Spalte 0.06. Der gesuchte z-Wert ist somit 1.96.
Bitte beachtet, dass es unterschiedliche Normalverteilungstabellen gibt und eure eventuell ganz anders aussieht. Die Vorgehensweise zum Finden des richtigen Quantils kann bei euch also auch ganz anders sein.
Details zur Normalverteilungstabelle
Um besser nachvollziehen zu können, was wir gerade ausgerechnet haben, hilft es sich zu erinnern, wie die Normalverteilung von oben aussieht:
In der Mitte auf der Höhe des Gipfels der Standardnormalverteilung befindet sich der Mittelwert, welcher 0 ist. Jetzt erkennt man leicht, was wir mit „symmetrischem Bereich“ gemeint haben, da die Verteilung symmetrisch ist. Der rechte Wert, bei dem der orange Bereich vom weißen Bereich getrennt wird, ist derselbe wie auf der linken Seite nur mit unterschiedlichem Vorzeichen. Daher hätten wir auch das Quantil berechnen können, bei dem 2.5% der Verteilung links und 97.5% rechts liegen. Das wäre das 2.5%-Quantil bzw. der z Wert an der Stelle 0.025. Ihr seht, dass dieser Wert auf der gegebenen Tabelle gar nicht drauf ist. Das ist der Fall, weil sie so konstruiert ist, dass sie nur positive z-Werte abbildet. Das 2.5%- Quantil hat nämlich denselben Wert, wie das 97.5%-Quantil nur negativ. Also -1.96. Daher reicht es, die Hälfte der z-Werte zu tabellieren und die passende Wahrscheinlichkeit zum Nachschlagen zu verwenden.
Quantil rechnerisch bestimmen
Rechnerisch sieht das Bestimmen des Quantils wie folgt aus. In unserer Formel steht \(z_{1-\frac{\alpha}{2}}\). \(\alpha\) ist ja bekanntlich das Signifikanzniveau. Wenn wir ein Konfidenzniveau von 0.95 gegeben haben, dann beträgt das Signifikanzniveau 0.05. Das heißt für \(\alpha\) setzen wir 0.05 ein.
$$z_{1-\frac{0.05}{2}} = z_{1-0.025} = z_{0.975} $$
Somit erhalten wir wie vorher den z-Wert von 0.975 und schauen diesen Wert erneut in der Tabelle nach, um 1.96 zu erhalten.
Ihr könnt also mit diesen beiden Methoden ganz einfach das korrekte Quantil herausfinden. In den meisten Fällen werden jedoch das 90, 95 und 99% Konfidenzintervall verwendet. Das heißt ihr könnt euch die folgenden Werte (auf 2 Nachkommastellen gerundet) auch einfach auswendig merken:
| Konfidenzintervall | z-Wert |
| 90% | 1.645 |
| 95% | 1.96 |
| 99% | 2.58 |
Konfidenzintervall bestimmen
Berechnen wir noch kurz den Standardfehler:
$$s = \sqrt{\frac{\widehat{p}-(1-\widehat{p})}{n}} = \sqrt{\frac{0.3-0.7}{500}} = 0.0205 $$
Jetzt haben wir alle Werte, die wir brauchen
$$\widehat{p} = 0.3 \quad z_{1-\frac{\alpha}{2}} = 1.96 \quad s = 0.0205$$
und wir können sie in die Formel einsetzen.
$$\begin{aligned} KI &= [\widehat{p} – z_{1-\frac{\alpha}{2}} \cdot s; \widehat{p} + z_{1-\frac{\alpha}{2}} \cdot s] \\ KI &= [0.3 – 1.96 \cdot 0.0205; 0.3 + 1.96 \cdot 0.0205] \\ KI &= [0.3 – 0.0402; 0.3 – 0.0402] \\ KI &= [0.2598; 0.3402]\end{aligned}$$
Wie im Erklärungsbeitrag schon erwähnt, stellt das Quantil * Standardfehler, also 0.0402 die Schwankungsbreite dar. Die Differenz von oberer zu unterer Grenze beschreibt die Länge des Intervalls.
Um die Länge zu erhalten, könnt ihr entweder besagte Differenz berechnen, oder noch einfacher ihr rechnet 2 Mal die Schwankungsbreite. Die Länge beträgt somit
$$\text{Länge des KI} = \text{obere Grenze} – \text{untere Grenze} = 0.3402 – 0.2598= 0.0804$$
$$\text{Länge des KI} = 2 \cdot \text{Schwankungsbreite} = 2 \cdot z_{1-\frac{\alpha}{2}} \cdot s = 2 \cdot 0.0402 = 0.0804$$
Interpretation
Hier könnt ihr die Hilfestellungen verwenden, die ich euch im Einleitungsvideo zu Konfidenzintervallen bereitgestellt habe.
Mit so und so viel prozentiger Sicherheit, liegt der wahre Wert zwischen unterer und oberer Grenze.
In diesem Fall heißt das also, dass der wahre Anteil der Wahlberechtigten, die für unsere Partei stimmen mit 95-prozentiger Sicherheit zwischen 25.98 und 34.02 Prozent liegt.
Es gibt natürlich mehrere Möglichkeiten die Interpretation zu formulieren, mehr dazu findet ihr im Erklärungsbeitrag zu Konfidenzintervallen.
