Tauche ein in unsere modebewusste Statistik-Welt.
Kombinatorik – Permutation
- Was ist eine Permutation?
- Permutation mit/ohne Wiederholung
- Formel herleiten
- Viele Beispiele
Ihr solltet auf jeden Fall bereits den Beitrag zu Variation und Kombination gelesen haben. Viele Begriffe werden hier nicht mehr näher erläutert.
Was ist eine Permutation?
Wir bestimmen die Anzahl aller möglicher Anordnungen durch eine Permutation, wenn wir alle Elemente einer Menge betrachten, also keine Auswahl treffen. Zum Beispiel, auf wie viele verschiedene Arten können drei unterschiedliche Buchstaben angeordnet werden.
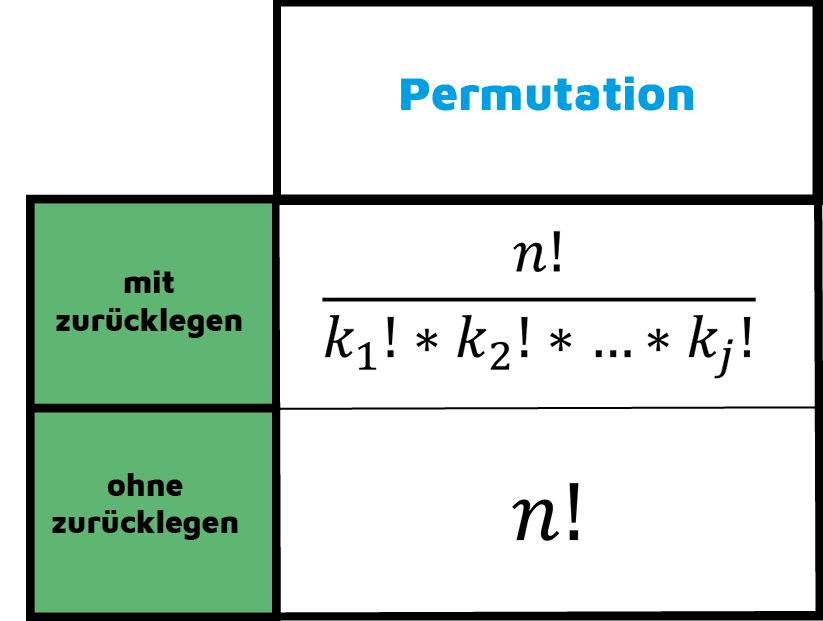
Wir unterscheiden zwischen Permutation mit und ohne Wiederholung. Mit Wiederholung oder mit Zurücklegen haben wir, wenn wir gezogene Elemente wieder zurückgeben und somit immer dieselbe Anzahl an Elementen in der Grundgesamtheit haben. Wenn ich zum Beispiel eine Kugel aus einer Urne ziehe und diese wieder zurücklege nach der Ziehung, handelt es sich um eine Ziehung mit Wiederholung. Wenn ich die Kugel nicht zurückgebe, verändert sich die Menge ständig und das wäre dann eine Ziehung ohne Wiederholung.
Permutation ohne Wiederholung
Wir sehen uns zuerst ein Beispiel für Permutation ohne Wiederholung an.
Stellen wir uns vor, wir haben 4 freie Parkplätze und wir wollen wissen, wie viele Möglichkeiten es gibt, 4 Autos auf diese freien Stellflächen aufzuteilen. Es werden alle Elemente (= Autos) verwendet, somit haben wir keine Auswahl getroffen. Wenn wir ein Auto geparkt haben, dann ist dieser Parkplatz voll und kann nicht erneut als Parkplatz ausgewählt werden. Somit können wir sagen, der Prozess funktioniert ohne Zurücklegen und deswegen haben wir also eine Permutation ohne Wiederholung.
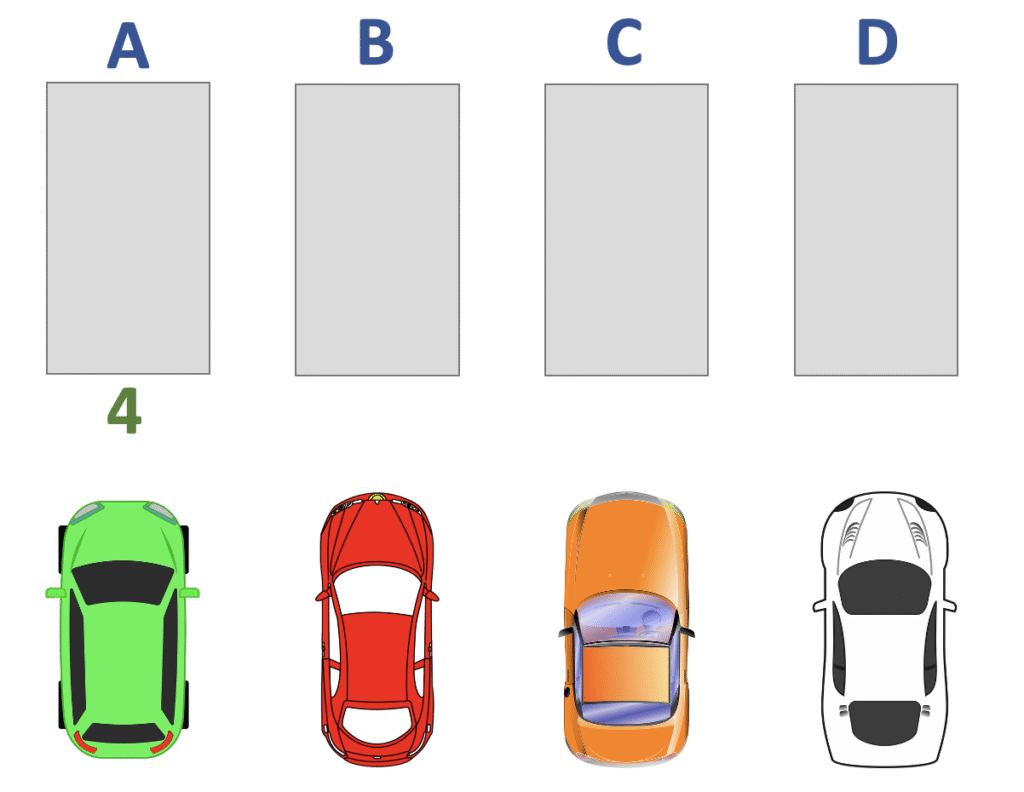
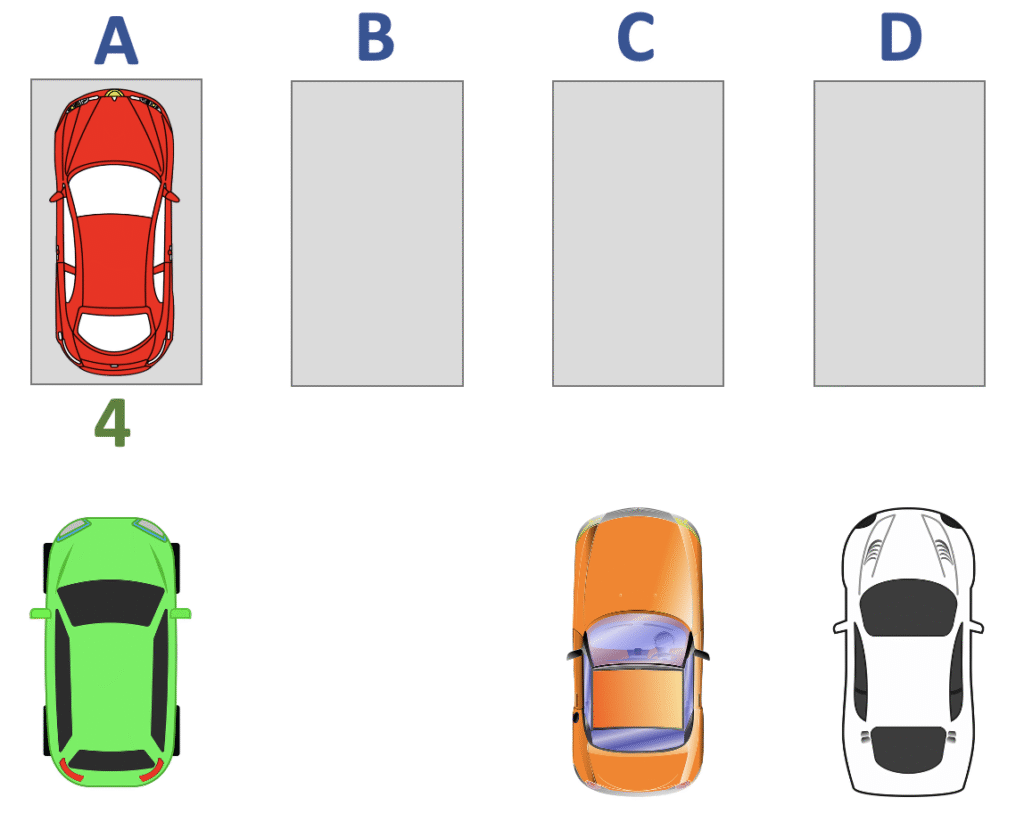
Für den ersten Parkplatz haben wir also 4 Autos zur Auswahl. Stellen wir nun ein Auto auf den freien Platz, dann bleiben natürlich nur mehr 3 Autos übrig.
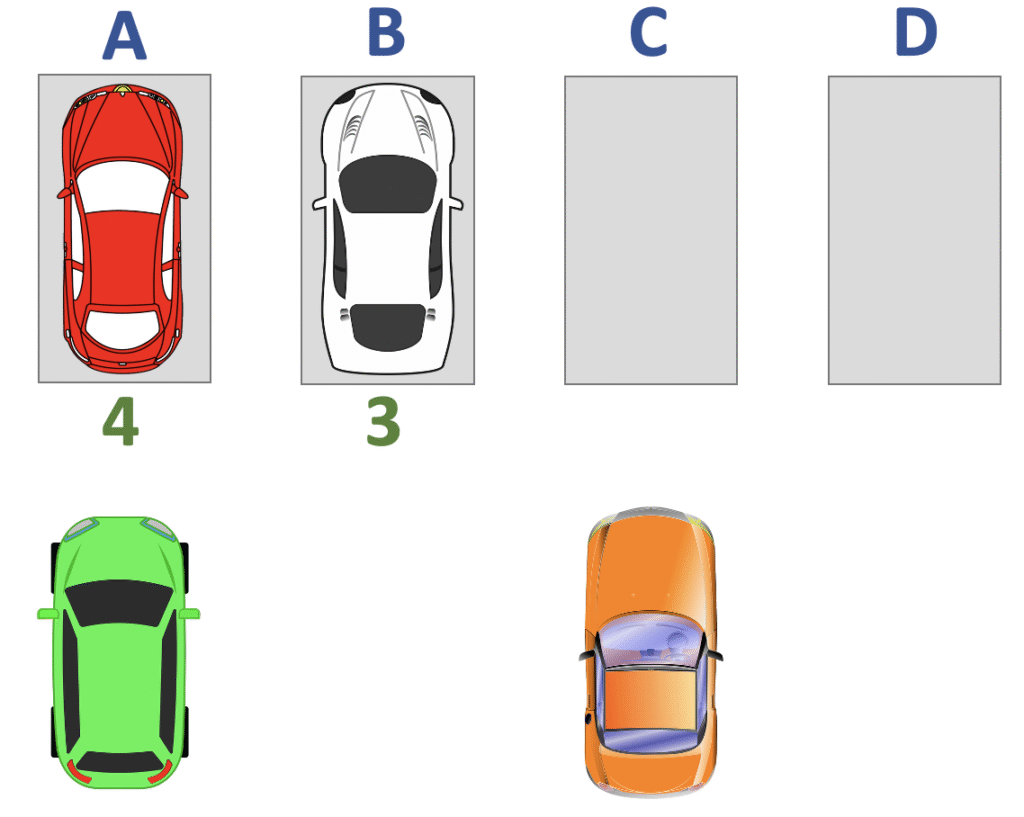
Stellen wir das nächste Auto auf den zweiten Parkplatz, dann haben wir noch 2 Autos zur Auswahl.
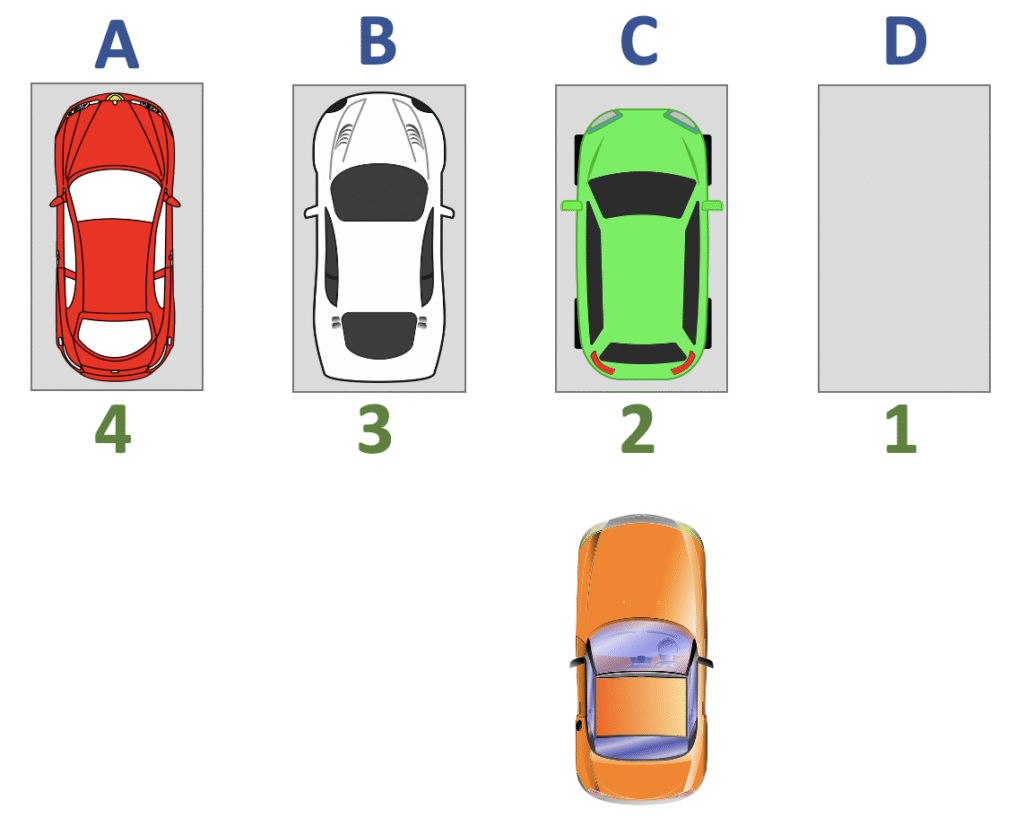
Zum Schluss haben wir nur noch eine Möglichkeit.
Somit haben wir \(4 \cdot 3 \cdot 2 \cdot 1 = 24\) verschiedene Möglichkeiten unsere Autos anzuordnen.
Herleitung der Formel
Durch diese Überlegung können wir uns die Formel für Permutation ohne Wiederholung mühelos eigenständig herleiten.
Wir hatten ja n=4 Autos. Somit stehen uns für den ersten Platz n Autos zur Verfügung. Für den zweiten Parkplatz konnten wir 1 Auto weniger auswählen – oder anders ausgedrückt, wir konnten n-1 Autos auswählen.
In weiterer Folge reduzieren sich die Auswahlmöglichkeiten weiter. Wir haben n-2 Möglichkeiten für den dritten Platz und n-3 für den vierten Parkplatz.
Diese Abfolge von Auswahlmöglichkeiten lässt sich als Produkt \(n \cdot (n-1) \cdot (n-2) \cdot (n-3)\) darstellen, was wiederum gleichbedeutend mit n Fakultät (n!) ist.
So habt ihr euch die Formel schnell und einfach selbst abgeleitet und könnt in Zukunft solche Aufgaben direkt mit der Formel lösen.
Wir hatten 4 Autos, somit müssen wir nur 4! rechnen, was wiederum \(4 \cdot 3 \cdot 2 \cdot 1 = 24\) Möglichkeiten ergibt.
Beispiel
Zur Verdeutlichung kurz ein zweites Beispiel. Wir haben das Wort „MARKE“. Wie viele Möglichkeiten gibt es, die Buchstaben anders anzuordnen?
Wir verwenden alle Buchstaben, somit treffen wir keine Auswahl. Jeder Buchstabe kommt nur einmal vor, deswegen haben wir also erneut Permutation ohne Zurücklegen und die korrekte Formel ist n! wobei n = 5 ist, da „MARKE“ 5 Buchstaben hat.
$$n! = 5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120$$
Es gibt also 120 mögliche Anordnungen der 5 Buchstaben.
Permutation mit Wiederholung
Sehen wir uns dazu direkt ein ähnliches Beispiel an, das aber ein anderes Wort verwendet. Wie viele Möglichkeiten gibt es, die Buchstaben des Wortes „STATISTIK“ anzuordnen?
Der wesentliche Unterschied besteht darin, dass im vorherigen Fall, beim Wort „MARKE“, jeder Buchstabe nur einmal vorkam. Jetzt haben wir es mit einer Permutation mit Wiederholung zu tun.
Das Wort „STATISTIK“ hat 3 „T“, 2 „S“, 2 „I“, 1 „A“ und 1 „K“. Würden wir zum Beispiel die 3 „T“ (TTT) als unterschiedliche Buchstaben betrachten, könnten wir sie wie soeben gelernt auf 3! (= 6) verschiedene Arten anordnen. Wie ihr seht, macht es aber keinen Unterschied, welches dieser 3 „T“ an der 1., 2. oder 3. Stelle steht.
Da es jetzt also 3-mal derselbe Buchstabe ist, habe ich nicht 6 Möglichkeiten, wie ich TTT aufschreiben kann, sondern nur 1.
Wir berechnen jetzt zuerst alle Möglichkeiten so wie zuvor mit n Fakultät. Wir haben 9 Buchstaben, also 9! (= 362880) mögliche Anordnungen der Buchstaben.
Da wir nur 1 mögliche Anordnung der „T“ anstelle von 6 haben, müssen wir diese Möglichkeiten noch aus dem Ergebnis herausrechnen. Die 3 „T“ können natürlich jetzt an jeder Stelle des Wortes vorkommen, das heißt wir müssen das Ergebnis durch 3! dividieren.
Dasselbe machen wir für die restlichen mehrfach vorkommenden Buchstaben 2 „S“ und 2 „I“. Der Vollständigkeit halber schreiben wir die Anordnungsmöglichkeiten der einzelnen Buchstaben „A“ und „K“ auch noch mit auf. (es gibt natürlich nur 1 Anordnungsmöglichkeit bei einem einzelnen Buchstaben)
$$\frac{362880}{3! \cdot 2! \cdot 2! \cdot 1! \cdot 1!} = 15120$$
Das führt dann zum Ergebnis von 15120 Anordnungen für die Buchstaben des Wortes „STATISTIK“.
Hergeleitete Formel
Das gerade hergeleitete Konzept können wir in einer Formel allgemein aufschreiben.
$$\frac{n!}{k_1! \cdot k_2! \cdot …\cdot k_j!}$$
Hier bezeichnet \(k_1\) die Anzahl, wie oft der Buchstabe 1 vorkommt, \(k_2\) die Anzahl, wie oft der Buchstabe 2 vorkommt usw.
Beispiele
Stellt euch vor, wir haben 12 Personen und in einem Hotel ein Vierbettzimmer, 2 Dreibettzimmer und ein Doppelzimmer zur Verfügung. Wir wollen die Möglichkeiten berechnen, die 12 Personen auf die Zimmer aufzuteilen
Man kann sich diese Situation vorstellen, als würde man die Zimmer den Personen zuteilten. Anders als bei den Parkplätzen vorher können hier mehrere Personen im selben Zimmer schlafen. (Daher mit Wiederholung)
Ob jetzt Person 1, Person 6, Person 2 und Person 10 das Vierbettzimmer zugeteilt wird oder Person 10, Person 1, Person 2 und Person 6 macht natürlich keinen Unterschied, daher müssen auch hier wieder redundante Zuordnungen aus der Gesamtzahl der möglichen Zuordnungen herausrechnen.
Das heißt
$$k_1 = 4, \quad k_2 = 3, \quad k_3 = 3, \quad k_4 = 2$$
Da wir 12 Personen haben, ist n = 12 und wir können alle Elemente in die Formel einsetzten:
$$\frac{12!}{4! \cdot 3! \cdot 3! \cdot 2!} = 277200$$
Es gibt also 277200 Möglichkeiten, die gegebenen Hotelzimmer unseren 12 Personen zuzuordnen.
Als zweites Beispiel haben wir ein Kartenspiel mit 4 Personen. Unser Kartendeck mit 52 Karten setzt sich aus 4 Farben mit jeweils 13 Karten je Farbe zusammen. Wie viele unterschiedliche Möglichkeiten gibt es, das gesamte Kartendeck auf die Personen aufzuteilen, wenn jede Person gleich viele Karten erhält?
Wir teilen alle Karten auf, somit erhält jede Person jeweils 13 Karten. Das bedeutet, wir haben jeweils 4 Partitionen zu jeweils 13 Karten. Die Teilmengen \(k_1\) bis \(k_4\) entsprechen also jeweils 13. Insgesamt haben wir n=52 Karten und die möglichen Anordnungen lassen sich also wieder wie vorher bestimmen:
$$\frac{52!}{13! \cdot 13! \cdot 13! \cdot 13!} = 5.36 \cdot 10^{28}$$
Es gibt also sehr, sehr viele Möglichkeiten, die Karten aufzuteilen.
Kombinatorik – Permutation
- Was ist eine Permutation?
- Permutation mit/ohne Wiederholung
- Formel herleiten
- Viele Beispiele
Ihr solltet auf jeden Fall bereits den Beitrag zu Variation und Kombination gelesen haben. Viele Begriffe werden hier nicht mehr näher erläutert.
Was ist eine Permutation?
Wir bestimmen die Anzahl aller möglicher Anordnungen durch eine Permutation, wenn wir alle Elemente einer Menge betrachten, also keine Auswahl treffen. Zum Beispiel, auf wie viele verschiedene Arten können drei unterschiedliche Buchstaben angeordnet werden.
Wir unterscheiden zwischen Permutation mit und ohne Wiederholung. Mit Wiederholung oder mit Zurücklegen haben wir, wenn wir gezogene Elemente wieder zurückgeben und somit immer dieselbe Anzahl an Elementen in der Grundgesamtheit haben. Wenn ich zum Beispiel eine Kugel aus einer Urne ziehe und diese wieder zurücklege nach der Ziehung, handelt es sich um eine Ziehung mit Wiederholung. Wenn ich die Kugel nicht zurückgebe, verändert sich die Menge ständig und das wäre dann eine Ziehung ohne Wiederholung.

Permutation ohne Wiederholung
Wir sehen uns zuerst ein Beispiel für Permutation ohne Wiederholung an.
Stellen wir uns vor, wir haben 4 freie Parkplätze und wir wollen wissen, wie viele Möglichkeiten es gibt, 4 Autos auf diese freien Stellflächen aufzuteilen. Es werden alle Elemente (= Autos) verwendet, somit haben wir keine Auswahl getroffen. Wenn wir ein Auto geparkt haben, dann ist dieser Parkplatz voll und kann nicht erneut als Parkplatz ausgewählt werden. Somit können wir sagen, der Prozess funktioniert ohne Zurücklegen und deswegen haben wir also eine Permutation ohne Wiederholung.


Für den ersten Parkplatz haben wir also 4 Autos zur Auswahl. Stellen wir nun ein Auto auf den freien Platz, dann bleiben natürlich nur mehr 3 Autos übrig.

Stellen wir das nächste Auto auf den zweiten Parkplatz, dann haben wir noch 2 Autos zur Auswahl.

Zum Schluss haben wir nur noch eine Möglichkeit.
Somit haben wir \(4 \cdot 3 \cdot 2 \cdot 1 = 24\) verschiedene Möglichkeiten unsere Autos anzuordnen.
Herleitung der Formel
Durch diese Überlegung können wir uns die Formel für Permutation ohne Wiederholung mühelos eigenständig herleiten.
Wir hatten ja n=4 Autos. Somit stehen uns für den ersten Platz n Autos zur Verfügung. Für den zweiten Parkplatz konnten wir 1 Auto weniger auswählen – oder anders ausgedrückt, wir konnten n-1 Autos auswählen.
In weiterer Folge reduzieren sich die Auswahlmöglichkeiten weiter. Wir haben n-2 Möglichkeiten für den dritten Platz und n-3 für den vierten Parkplatz.
Diese Abfolge von Auswahlmöglichkeiten lässt sich als Produkt \(n \cdot (n-1) \cdot (n-2) \cdot (n-3)\) darstellen, was wiederum gleichbedeutend mit n Fakultät (n!) ist.
So habt ihr euch die Formel schnell und einfach selbst abgeleitet und könnt in Zukunft solche Aufgaben direkt mit der Formel lösen.
Wir hatten 4 Autos, somit müssen wir nur 4! rechnen, was wiederum \(4 \cdot 3 \cdot 2 \cdot 1 = 24\) Möglichkeiten ergibt.
Beispiel
Zur Verdeutlichung kurz ein zweites Beispiel. Wir haben das Wort „MARKE“. Wie viele Möglichkeiten gibt es, die Buchstaben anders anzuordnen?
Wir verwenden alle Buchstaben, somit treffen wir keine Auswahl. Jeder Buchstabe kommt nur einmal vor, deswegen haben wir also erneut Permutation ohne Zurücklegen und die korrekte Formel ist n! wobei n = 5 ist, da „MARKE“ 5 Buchstaben hat.
$$n! = 5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120$$
Es gibt also 120 mögliche Anordnungen der 5 Buchstaben.
Permutation mit Wiederholung
Sehen wir uns dazu direkt ein ähnliches Beispiel an, das aber ein anderes Wort verwendet. Wie viele Möglichkeiten gibt es, die Buchstaben des Wortes „STATISTIK“ anzuordnen?
Der wesentliche Unterschied besteht darin, dass im vorherigen Fall, beim Wort „MARKE“, jeder Buchstabe nur einmal vorkam. Jetzt haben wir es mit einer Permutation mit Wiederholung zu tun.
Das Wort „STATISTIK“ hat 3 „T“, 2 „S“, 2 „I“, 1 „A“ und 1 „K“. Würden wir zum Beispiel die 3 „T“ (TTT) als unterschiedliche Buchstaben betrachten, könnten wir sie wie soeben gelernt auf 3! (= 6) verschiedene Arten anordnen. Wie ihr seht, macht es aber keinen Unterschied, welches dieser 3 „T“ an der 1., 2. oder 3. Stelle steht.
Da es jetzt also 3-mal derselbe Buchstabe ist, habe ich nicht 6 Möglichkeiten, wie ich TTT aufschreiben kann, sondern nur 1.
Wir berechnen jetzt zuerst alle Möglichkeiten so wie zuvor mit n Fakultät. Wir haben 9 Buchstaben, also 9! (= 362880) mögliche Anordnungen der Buchstaben.
Da wir nur 1 mögliche Anordnung der „T“ anstelle von 6 haben, müssen wir diese Möglichkeiten noch aus dem Ergebnis herausrechnen. Die 3 „T“ können natürlich jetzt an jeder Stelle des Wortes vorkommen, das heißt wir müssen das Ergebnis durch 3! dividieren.
Dasselbe machen wir für die restlichen mehrfach vorkommenden Buchstaben 2 „S“ und 2 „I“. Der Vollständigkeit halber schreiben wir die Anordnungsmöglichkeiten der einzelnen Buchstaben „A“ und „K“ auch noch mit auf. (es gibt natürlich nur 1 Anordnungsmöglichkeit bei einem einzelnen Buchstaben)
$$\frac{362880}{3! \cdot 2! \cdot 2! \cdot 1! \cdot 1!} = 15120$$
Das führt dann zum Ergebnis von 15120 Anordnungen für die Buchstaben des Wortes „STATISTIK“.
Hergeleitete Formel
Das gerade hergeleitete Konzept können wir in einer Formel allgemein aufschreiben.
$$\frac{n!}{k_1! \cdot k_2! \cdot …\cdot k_j!}$$
Hier bezeichnet \(k_1\) die Anzahl, wie oft der Buchstabe 1 vorkommt, \(k_2\) die Anzahl, wie oft der Buchstabe 2 vorkommt usw.
Beispiele
Stellt euch vor, wir haben 12 Personen und in einem Hotel ein Vierbettzimmer, 2 Dreibettzimmer und ein Doppelzimmer zur Verfügung. Wir wollen die Möglichkeiten berechnen, die 12 Personen auf die Zimmer aufzuteilen
Man kann sich diese Situation vorstellen, als würde man die Zimmer den Personen zuteilten. Anders als bei den Parkplätzen vorher können hier mehrere Personen im selben Zimmer schlafen. (Daher mit Wiederholung)
Ob jetzt Person 1, Person 6, Person 2 und Person 10 das Vierbettzimmer zugeteilt wird oder Person 10, Person 1, Person 2 und Person 6 macht natürlich keinen Unterschied, daher müssen auch hier wieder redundante Zuordnungen aus der Gesamtzahl der möglichen Zuordnungen herausrechnen.
Das heißt
$$k_1 = 4, \quad k_2 = 3, \quad k_3 = 3, \quad k_4 = 2$$
Da wir 12 Personen haben, ist n = 12 und wir können alle Elemente in die Formel einsetzten:
$$\frac{12!}{4! \cdot 3! \cdot 3! \cdot 2!} = 277200$$
Es gibt also 277200 Möglichkeiten, die gegebenen Hotelzimmer unseren 12 Personen zuzuordnen.
Als zweites Beispiel haben wir ein Kartenspiel mit 4 Personen. Unser Kartendeck mit 52 Karten setzt sich aus 4 Farben mit jeweils 13 Karten je Farbe zusammen. Wie viele unterschiedliche Möglichkeiten gibt es, das gesamte Kartendeck auf die Personen aufzuteilen, wenn jede Person gleich viele Karten erhält?
Wir teilen alle Karten auf, somit erhält jede Person jeweils 13 Karten. Das bedeutet, wir haben jeweils 4 Partitionen zu jeweils 13 Karten. Die Teilmengen \(k_1\) bis \(k_4\) entsprechen also jeweils 13. Insgesamt haben wir n=52 Karten und die möglichen Anordnungen lassen sich also wieder wie vorher bestimmen:
$$\frac{52!}{13! \cdot 13! \cdot 13! \cdot 13!} = 5.36 \cdot 10^{28}$$
Es gibt also sehr, sehr viele Möglichkeiten, die Karten aufzuteilen.

Comment (1)
[…] Kombinatorik – Permutation […]