Tauche ein in unsere modebewusste Statistik-Welt.
Konfidenzintervalle – Erklärung
- Stichprobe vs. Population
- Punkt- vs. Intervallschätzung
- Verwendung und Aufbau
In diesem Beitrag findet ihr keine Berechnung von Konfidenzintervallen. Diese Berechnung wird in separaten Beiträgen behandelt. Zum besseren Verständnis solltet ihr aber zuerst diesen Beitrag gelesen haben, bevor ihr zum Rechnen weitergeht.
Definition
Konfidenzintervalle, auch Vertrauensintervalle genannt, sind Schätzungen für einen unbekannten Parameter. Bei Parametern handelt es sich um Populationswerte, die wir in der Regel nicht kennen.
Konzept der Stichprobe und Schätzung
Häufig wollen wir Aussagen über die Grundgesamtheit aka. Population treffen. Zum Beispiel, wie hoch der Wähleranteil einer Partei oder das durchschnittliche Einkommen einer Berufsgruppe ist. Um diesen Wert genau bestimmen zu können, müssten wir jede einzelne Person in unserer Grundgesamtheit befragen. Wie ihr euch schon vorstellen könnt, ist das meistens praktisch unmöglich und auch sonst wäre das mit einem hohen Kosten- und Zeitaufwand verbunden.
Was macht man also? Aus der Grundgesamtheit zieht man eine Stichprobe. Anhand dieser können nun die gesuchten Werte berechnet werden. Das Ziel ist es, Rückschlüsse auf die Population zu treffen. Die Stichprobe entspricht jedoch nicht exakt der Population. Deshalb muss bei diesen Rückschlüssen noch ein gewisser Fehler, eine gewisse Schwankung miteinkalkuliert werden.
Die Population ist also die Grundgesamtheit aller Merkmale, die untersucht werden sollen. Populationswerte werden generell Parameter genannt und in der Regel mit griechischen Buchstaben gekennzeichnet.
$$\mu, \sigma, \sigma^2, \theta, \beta$$
Die Stichprobe ist eine Teilmenge aus dieser Grundgesamtheit. Werte aus der Stichprobe werden generell Kennwerte genannt und mit lateinischen Buchstaben gekennzeichnet.
$$\bar{x}, s, s^2, p, b$$
Schätzungen dienen dazu, Informationen zu den Populationswerten, die ja (in der Regel) nicht bekannt sind, zu finden. Eine Punktschätzung stellt dabei einen konkreten Wert dar, während eine Intervallschätzung einen Bereich angibt, in dem der gesuchte Wert liegen soll.
Ein Beispiel für einen Punktschätzer wäre das arithmetische Mittel. Wir könnten zum Beispiel sagen, dass Studierende im Schnitt 20 Stunden pro Woche arbeiten. Wenn wir sagen, sie arbeiten zwischen 18 und 22 Stunden, dann handelt es sich um eine Intervallschätzung.
Verwendung von Punkt- vs. Intervallschätzung
Die Punktschätzung gibt uns also einen genauen Wert an. Warum sollte man trotzdem eine Intervallschätzung verwenden?
Punktschätzungen sind mit hoher Unsicherheit verbunden und zum Teil irreführend, weil sie eine nicht vorhandene Sicherheit implizieren. Bei einer Intervallschätzung ist es für den Betrachter eindeutiger, dass es sich um eine nicht gänzlich sichere Aussage handelt. Wenn wir jemandem sagen, wie lange wir noch zu einem vereinbarten Treffpunkt brauchen, sagen wir ja auch normalerweise 10-15 min anstatt 11:36 min, weil das natürlich schwer einzuhalten wäre.
Aufbau von Konfidenzintervallen
Konfidenzintervalle sind Intervallschätzungen für einen unbekannten Parameter. Dies kann ein Anteil, ein Mittelwert, ein Regressionskoeffizient oder vieles mehr sein. Egal, was geschätzt werden soll, Konfidenzintervalle sind immer gleich aufgebaut.
Die Struktur eines Konfidenzintervalls schaut so aus:
[Punktschätzer ± Quantil * Standardfehler]
Für einen Mittelwert würde die Formel für das Konfidenzintervall zum Beispiel wie folgt aussehen:
$$[\bar{x} \pm t_{1-\frac{\alpha}{2}} \cdot \frac{s}{\sqrt{n}}]$$
\(\bar{x}\) bezeichnet hier natürlich das ausgerechnete arithmetische Mittel, \( t_{1-\frac{\alpha}{2}}\) ist das \(1- \frac{\alpha}{2}\) der T-Verteilung, s stellt die ausgerechnete Standardabweichung dar und n ist die Stichprobengröße. Das nur, um es erwähnt zu haben. In den anderen Beiträgen zu den Konfidenzintervallen, gehen wir auf diese Komponenten näher ein.
Da Konfidenzintervalle Schätzungen sind, können wir nie zu 100 % garantieren, dass das Konfidenzintervall den gesuchten Parameter beinhaltet. Deshalb muss man bei Konfidenzintervallen immer eine Sicherheit, auch Konfidenzniveau genannt, bestimmen. Diese kann beliebig gewählt werden. Es haben sich aber die Werte 90, 95 und 99 % etabliert. Dieses Konfidenz- oder Signifikanzniveau beschreibt man durch den gr. Buchstaben \(\alpha\).
Sehen wir uns gleich anhand eines Beispiels an, was dies bedeutet. Stellen wir uns vor, wir sind Mitglied einer Partei und wir wollen wissen, wie hoch der Wähleranteil zum aktuellen Zeitpunkt ist. Um dies exakt feststellen zu können, müssten wir ja die gesamte Population befragen. Da dies nicht möglich oder zumindest äußerst aufwändig wäre, befragen wir eine Stichprobe, um anhand dieser den uns nicht bekannten Wähleranteil in der Population zu schätzen. Dazu berechnen wir ein 95% Konfidenzintervall.
Wir haben eine Stichprobe von 500 Personen befragt, und 150 davon würden die Partei wählen. Das entspricht 30% der Befragten und stellt auch gleichzeitig unsere Punktschätzung dar.
$$\hat{p} = 0.3$$
Wenn wir das Konfidenzintervall berechnen erhalten wir:
[0.3 ± 0.04]
Das ergibt einen Bereich von 0.26 bis 0.34 in dem unser unbekannter Parameter liegen soll.
[0.26, 0.34]
Einfach ausgedrückt heißt das, dass der Wähleranteil in der Population mit hoher Sicherheit zwischen 26 und 34 Prozent liegt. Auf die Interpretation gehen wir gleich noch näher ein.
Die 0.04 hinter dem Plus/Minus (±) nennt man Schwankungsbreite oder Fehlerspanne und die Differenz von unterer zu oberer Grenze stellt die Länge des Intervalls dar.
Wie man dieses Intervall berechnet, wird euch in den anderen Beiträgen zu Konfidenzintervallen genau erklärt.
Interpretation
Viele haben oft kein Problem ein Konfidenzintervall zu berechnen, meistens scheitert es daran, das Ergebnis korrekt zu interpretieren. Deshalb habe ich für euch hier eine kleine Interpretationshilfe vorbereitet. Es gibt natürlich viele Möglichkeiten ein Konfidenzintervall korrekt zu interpretieren, wenn ihr euch aber unsicher seid, könnt ihr folgende Vorlage verwenden:
Mit so und so viel prozentiger Sicherheit, liegt der wahre Wert zwischen unterer und oberer Grenze.
Hier noch einige Beispiele zur Veranschaulichung:
Das Ergebnis von vorhin war das Intervall [0.26, 0.34] und wir haben als Sicherheit 95% gewählt. Das heißt, laut unserer Schablone könnten wir das Intervall nun wie folgt interpretieren: Mit 95-prozentiger Sicherheit liegt der wahre Anteil der Wahlberechtigten, die für uns stimmen würden, zwischen 26 und 34%.
Bitte aufpassen! Das Konfidenzintervall sagt uns, dass der Populationswert mit hoher Sicherheit zwischen 26 und 34% liegen soll. Es sagt uns nicht, dass uns zwischen 26 und 34% der Leute sicher wählen.
Dieselbe Interpretation ist auch auf ein Konfidenzintervall mit Mittelwert als Punktschätzer anwendbar. Beim Beispiel vom Anfang haben wir gesagt, dass Studierende zwischen 18 und 22 Stunden in der Woche arbeiten. Sagen wir, wir hatten 99% als Sicherheit (bzw. Signifikanzniveau) gewählt. Wenn wir unsere Vorlage verwenden, würden wir sagen, dass mit 99-prozentiger Sicherheit der wahre Wert der wöchentlichen Arbeitszeit von Studierenden zwischen 18 und 22 Stunden liegt.
Statt 95-prozentiger Sicherheit könnt ihr auch 95-prozentiges Vertrauen oder in 95 von 100 Fällen sagen.
Mit dem wahren Wert ist der tatsächliche Anteil bzw. Wert in der Population gemeint, das heißt ihr könnt stattdessen auch Populationswert bzw. Populationsanteil sagen.
Wie ist das jetzt mit dieser Sicherheit?
Was ihr in Zusammenhang mit Konfidenzintervallen besser nicht machen sollt, ist, von einer Wahrscheinlichkeit zu sprechen. Dies geschieht sehr häufig, ist aber für viele Quellen nicht korrekt.
Wir wollen mittels Konfidenzintervall den Populationsparameter schätzen und auch wenn wir ihn nicht kennen, existiert er.
Das heißt, es gibt eigentlich nur zwei Möglichkeiten. Wir lagen mit unserer Schätzung richtig oder eben nicht. Anders ausgedrückt, der Populationswert kann nur entweder im Intervall oder außerhalb des Intervalls liegen. Was anderes ist ja gar nicht möglich! Deswegen kann die Wahrscheinlichkeit, dass der Populationswert im Intervall liegt, nur 0 oder 1, sprich 0 oder 100% sein.
Was bedeutet dann eine 95%ige Sicherheit genau? Die statistische Sicherheit sagt, dass wenn wir 100 gleich große Stichproben aus derselben Population ziehen und davon jeweils das Konfidenzintervall berechnen würden, 95 davon den wahren Wert beinhalten.
Um das zu veranschaulichen, nehmen wir an, den tatsächlichen Wähleranteil unserer Partei zu kennen. Dieser liegt bei 33%. Das Konfidenzintervall, das wir zuvor berechnet haben, beinhaltet also den wahren Anteil. Wenn wir erneut eine Stichprobe ziehen und das Konfidenzintervall von dieser neuen Stichprobe berechnen, könnten wir zum Beispiel ein Intervall erhalten, welches von 32 bis 40% geht. [0.32, 0.4]
Wenn wir wieder eine Stichprobe ziehen, das Intervall für diese berechnen, könnten wir als Grenzen 22 bis 30% erhalten. [0.22, 0.30]
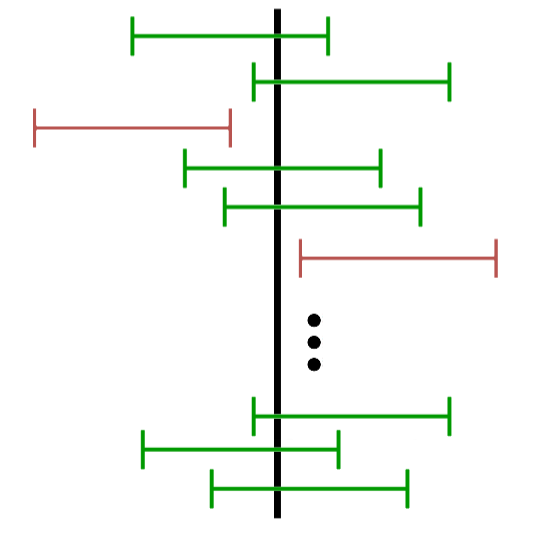
Das Ganze machen wir 100 Mal und bei 5 von diesen 100 Konfidenzintervallen würde der wahre Wert nun außerhalb des Intervalls liegen. Das entspricht dann einer 95-prozentigen Sicherheit.
Einflussfaktoren
Wir gehen noch kurz darauf ein, welche Parameter das Konfidenzintervall beeinflussen können.
Wir haben bisher immer von der Population gesprochen. Bei unserem Beispiel bestand die Population aus allen Wahlberechtigten eines bestimmten Landes. Hierbei kann es sich je nach Land um einige Tausend oder mehrere hundert Millionen handeln. Die Größe der Population spielt für die Berechnung des Konfidenzintervalls keine Rolle.
Die Parameter, die von uns gewählt werden können und das Konfidenzintervall beeinflussen, sind der Stichprobenumfang und die Sicherheit (= Signifikanzniveau).
Je größer der Stichprobenumfang ist, desto kleiner, sprich genauer wird das Konfidenzintervall. Das ist ja eigentlich ziemlich logisch, je mehr Personen ich befrage, desto besser kann ich Dinge einschätzen und somit wird die Schätzung genauer.
Je größer die Sicherheit ist, desto größer bzw. ungenauer wird das Konfidenzintervall. Das klingt nun für viele im ersten Moment widersprüchlich, macht aber bei genauerer Betrachtung viel Sinn.
Wenn ich für einen Populationswert ein Konfidenzintervall berechnen möchte, dann kommt es ja vor, dass sich dieser Wert nicht im Konfidenzintervall befindet. Wenn ich mit höherer Sicherheit haben will, dass sich der Populationswert im Intervall befindet, dann muss sich dieses Intervall vergrößern, damit der Wert noch im Intervall liegt. Doch ein größeres Konfidenzintervall bedeutet gleichzeitig eine höhere Ungenauigkeit. Wenn ich mir sicherer sein will, eine vereinbarte Zeit einhalten zu können, dann sage ich auch eher, ich komme innerhalb von einer Stunde anstatt innerhalb der nächsten 10 Minuten.
Konfidenzintervalle – Erklärung
- Stichprobe vs. Population
- Punkt- vs. Intervallschätzung
- Verwendung und Aufbau
In diesem Beitrag findet ihr keine Berechnung von Konfidenzintervallen. Diese Berechnung wird in separaten Beiträgen behandelt. Zum besseren Verständnis solltet ihr aber zuerst diesen Beitrag gelesen haben, bevor ihr zum Rechnen weitergeht.
Definition
Konfidenzintervalle, auch Vertrauensintervalle genannt, sind Schätzungen für einen unbekannten Parameter. Bei Parametern handelt es sich um Populationswerte, die wir in der Regel nicht kennen.
Konzept der Stichprobe und Schätzung
Häufig wollen wir Aussagen über die Grundgesamtheit aka. Population treffen. Zum Beispiel, wie hoch der Wähleranteil einer Partei oder das durchschnittliche Einkommen einer Berufsgruppe ist. Um diesen Wert genau bestimmen zu können, müssten wir jede einzelne Person in unserer Grundgesamtheit befragen. Wie ihr euch schon vorstellen könnt, ist das meistens praktisch unmöglich und auch sonst wäre das mit einem hohen Kosten- und Zeitaufwand verbunden.
Was macht man also? Aus der Grundgesamtheit zieht man eine Stichprobe. Anhand dieser können nun die gesuchten Werte berechnet werden. Das Ziel ist es, Rückschlüsse auf die Population zu treffen. Die Stichprobe entspricht jedoch nicht exakt der Population. Deshalb muss bei diesen Rückschlüssen noch ein gewisser Fehler, eine gewisse Schwankung miteinkalkuliert werden.
Die Population ist also die Grundgesamtheit aller Merkmale, die untersucht werden sollen. Populationswerte werden generell Parameter genannt und in der Regel mit griechischen Buchstaben gekennzeichnet.
$$\mu, \sigma, \sigma^2, \theta, \beta$$
Die Stichprobe ist eine Teilmenge aus dieser Grundgesamtheit. Werte aus der Stichprobe werden generell Kennwerte genannt und mit lateinischen Buchstaben gekennzeichnet.
$$\bar{x}, s, s^2, p, b$$
Schätzungen dienen dazu, Informationen zu den Populationswerten, die ja (in der Regel) nicht bekannt sind, zu finden. Eine Punktschätzung stellt dabei einen konkreten Wert dar, während eine Intervallschätzung einen Bereich angibt, in dem der gesuchte Wert liegen soll.
Ein Beispiel für einen Punktschätzer wäre das arithmetische Mittel. Wir könnten zum Beispiel sagen, dass Studierende im Schnitt 20 Stunden pro Woche arbeiten. Wenn wir sagen, sie arbeiten zwischen 18 und 22 Stunden, dann handelt es sich um eine Intervallschätzung.
Verwendung von Punkt- vs. Intervallschätzung
Die Punktschätzung gibt uns also einen genauen Wert an. Warum sollte man trotzdem eine Intervallschätzung verwenden?
Punktschätzungen sind mit hoher Unsicherheit verbunden und zum Teil irreführend, weil sie eine nicht vorhandene Sicherheit implizieren. Bei einer Intervallschätzung ist es für den Betrachter eindeutiger, dass es sich um eine nicht gänzlich sichere Aussage handelt. Wenn wir jemandem sagen, wie lange wir noch zu einem vereinbarten Treffpunkt brauchen, sagen wir ja auch normalerweise 10-15 min anstatt 11:36 min, weil das natürlich schwer einzuhalten wäre.
Aufbau von Konfidenzintervallen
Konfidenzintervalle sind Intervallschätzungen für einen unbekannten Parameter. Dies kann ein Anteil, ein Mittelwert, ein Regressionskoeffizient oder vieles mehr sein. Egal, was geschätzt werden soll, Konfidenzintervalle sind immer gleich aufgebaut.
Die Struktur eines Konfidenzintervalls schaut so aus:
[Punktschätzer ± Quantil * Standardfehler]
Für einen Mittelwert würde die Formel für das Konfidenzintervall zum Beispiel wie folgt aussehen:
$$[\bar{x} \pm t_{1-\frac{\alpha}{2}} \cdot \frac{s}{\sqrt{n}}]$$
\(\bar{x}\) bezeichnet hier natürlich das ausgerechnete arithmetische Mittel, \( t_{1-\frac{\alpha}{2}}\) ist das \(1- \frac{\alpha}{2}\) der T-Verteilung, s stellt die ausgerechnete Standardabweichung dar und n ist die Stichprobengröße. Das nur, um es erwähnt zu haben. In den anderen Beiträgen zu den Konfidenzintervallen, gehen wir auf diese Komponenten näher ein.
Da Konfidenzintervalle Schätzungen sind, können wir nie zu 100 % garantieren, dass das Konfidenzintervall den gesuchten Parameter beinhaltet. Deshalb muss man bei Konfidenzintervallen immer eine Sicherheit, auch Konfidenzniveau genannt, bestimmen. Diese kann beliebig gewählt werden. Es haben sich aber die Werte 90, 95 und 99 % etabliert. Dieses Konfidenz- oder Signifikanzniveau beschreibt man durch den gr. Buchstaben \(\alpha\).
Sehen wir uns gleich anhand eines Beispiels an, was dies bedeutet. Stellen wir uns vor, wir sind Mitglied einer Partei und wir wollen wissen, wie hoch der Wähleranteil zum aktuellen Zeitpunkt ist. Um dies exakt feststellen zu können, müssten wir ja die gesamte Population befragen. Da dies nicht möglich oder zumindest äußerst aufwändig wäre, befragen wir eine Stichprobe, um anhand dieser den uns nicht bekannten Wähleranteil in der Population zu schätzen. Dazu berechnen wir ein 95% Konfidenzintervall.
Wir haben eine Stichprobe von 500 Personen befragt, und 150 davon würden die Partei wählen. Das entspricht 30% der Befragten und stellt auch gleichzeitig unsere Punktschätzung dar.
$$\hat{p} = 0.3$$
Wenn wir das Konfidenzintervall berechnen erhalten wir:
[0.3 ± 0.04]
Das ergibt einen Bereich von 0.26 bis 0.34 in dem unser unbekannter Parameter liegen soll.
[0.26, 0.34]
Einfach ausgedrückt heißt das, dass der Wähleranteil in der Population mit hoher Sicherheit zwischen 26 und 34 Prozent liegt. Auf die Interpretation gehen wir gleich noch näher ein.
Die 0.04 hinter dem Plus/Minus (±) nennt man Schwankungsbreite oder Fehlerspanne und die Differenz von unterer zu oberer Grenze stellt die Länge des Intervalls dar.
Wie man dieses Intervall berechnet, wird euch in den anderen Beiträgen zu Konfidenzintervallen genau erklärt.
Interpretation
Viele haben oft kein Problem ein Konfidenzintervall zu berechnen, meistens scheitert es daran, das Ergebnis korrekt zu interpretieren. Deshalb habe ich für euch hier eine kleine Interpretationshilfe vorbereitet. Es gibt natürlich viele Möglichkeiten ein Konfidenzintervall korrekt zu interpretieren, wenn ihr euch aber unsicher seid, könnt ihr folgende Vorlage verwenden:
Mit so und so viel prozentiger Sicherheit, liegt der wahre Wert zwischen unterer und oberer Grenze.
Hier noch einige Beispiele zur Veranschaulichung:
Das Ergebnis von vorhin war das Intervall [0.26, 0.34] und wir haben als Sicherheit 95% gewählt. Das heißt, laut unserer Schablone könnten wir das Intervall nun wie folgt interpretieren: Mit 95-prozentiger Sicherheit liegt der wahre Anteil der Wahlberechtigten, die für uns stimmen würden, zwischen 26 und 34%.
Bitte aufpassen! Das Konfidenzintervall sagt uns, dass der Populationswert mit hoher Sicherheit zwischen 26 und 34% liegen soll. Es sagt uns nicht, dass uns zwischen 26 und 34% der Leute sicher wählen.
Dieselbe Interpretation ist auch auf ein Konfidenzintervall mit Mittelwert als Punktschätzer anwendbar. Beim Beispiel vom Anfang haben wir gesagt, dass Studierende zwischen 18 und 22 Stunden in der Woche arbeiten. Sagen wir, wir hatten 99% als Sicherheit (bzw. Signifikanzniveau) gewählt. Wenn wir unsere Vorlage verwenden, würden wir sagen, dass mit 99-prozentiger Sicherheit der wahre Wert der wöchentlichen Arbeitszeit von Studierenden zwischen 18 und 22 Stunden liegt.
Statt 95-prozentiger Sicherheit könnt ihr auch 95-prozentiges Vertrauen oder in 95 von 100 Fällen sagen.
Mit dem wahren Wert ist der tatsächliche Anteil bzw. Wert in der Population gemeint, das heißt ihr könnt stattdessen auch Populationswert bzw. Populationsanteil sagen.
Wie ist das jetzt mit dieser Sicherheit?
Was ihr in Zusammenhang mit Konfidenzintervallen besser nicht machen sollt, ist, von einer Wahrscheinlichkeit zu sprechen. Dies geschieht sehr häufig, ist aber für viele Quellen nicht korrekt.
Wir wollen mittels Konfidenzintervall den Populationsparameter schätzen und auch wenn wir ihn nicht kennen, existiert er.
Das heißt, es gibt eigentlich nur zwei Möglichkeiten. Wir lagen mit unserer Schätzung richtig oder eben nicht. Anders ausgedrückt, der Populationswert kann nur entweder im Intervall oder außerhalb des Intervalls liegen. Was anderes ist ja gar nicht möglich! Deswegen kann die Wahrscheinlichkeit, dass der Populationswert im Intervall liegt, nur 0 oder 1, sprich 0 oder 100% sein.
Was bedeutet dann eine 95%ige Sicherheit genau? Die statistische Sicherheit sagt, dass wenn wir 100 gleich große Stichproben aus derselben Population ziehen und davon jeweils das Konfidenzintervall berechnen würden, 95 davon den wahren Wert beinhalten.
Um das zu veranschaulichen, nehmen wir an, den tatsächlichen Wähleranteil unserer Partei zu kennen. Dieser liegt bei 33%. Das Konfidenzintervall, das wir zuvor berechnet haben, beinhaltet also den wahren Anteil. Wenn wir erneut eine Stichprobe ziehen und das Konfidenzintervall von dieser neuen Stichprobe berechnen, könnten wir zum Beispiel ein Intervall erhalten, welches von 32 bis 40% geht. [0.32, 0.4]
Wenn wir wieder eine Stichprobe ziehen, das Intervall für diese berechnen, könnten wir als Grenzen 22 bis 30% erhalten. [0.22, 0.30]

Das Ganze machen wir 100 Mal und bei 5 von diesen 100 Konfidenzintervallen würde der wahre Wert nun außerhalb des Intervalls liegen. Das entspricht dann einer 95-prozentigen Sicherheit.
Einflussfaktoren
Wir gehen noch kurz darauf ein, welche Parameter das Konfidenzintervall beeinflussen können.
Wir haben bisher immer von der Population gesprochen. Bei unserem Beispiel bestand die Population aus allen Wahlberechtigten eines bestimmten Landes. Hierbei kann es sich je nach Land um einige Tausend oder mehrere hundert Millionen handeln. Die Größe der Population spielt für die Berechnung des Konfidenzintervalls keine Rolle.
Die Parameter, die von uns gewählt werden können und das Konfidenzintervall beeinflussen, sind der Stichprobenumfang und die Sicherheit (= Signifikanzniveau).
Je größer der Stichprobenumfang ist, desto kleiner, sprich genauer wird das Konfidenzintervall. Das ist ja eigentlich ziemlich logisch, je mehr Personen ich befrage, desto besser kann ich Dinge einschätzen und somit wird die Schätzung genauer.
Je größer die Sicherheit ist, desto größer bzw. ungenauer wird das Konfidenzintervall. Das klingt nun für viele im ersten Moment widersprüchlich, macht aber bei genauerer Betrachtung viel Sinn.
Wenn ich für einen Populationswert ein Konfidenzintervall berechnen möchte, dann kommt es ja vor, dass sich dieser Wert nicht im Konfidenzintervall befindet. Wenn ich mit höherer Sicherheit haben will, dass sich der Populationswert im Intervall befindet, dann muss sich dieses Intervall vergrößern, damit der Wert noch im Intervall liegt. Doch ein größeres Konfidenzintervall bedeutet gleichzeitig eine höhere Ungenauigkeit. Wenn ich mir sicherer sein will, eine vereinbarte Zeit einhalten zu können, dann sage ich auch eher, ich komme innerhalb von einer Stunde anstatt innerhalb der nächsten 10 Minuten.

Comment (1)
[…] Grundlagen zu Konfidenzintervallen werden im Beitrag Konfidenzintervalle – Erklärung genauer beschrieben. Das Wissen in diesem Beitrag wird hier […]