Tauche ein in unsere modebewusste Statistik-Welt.
Median
Hier betrachten wir ein weiteres Lagemaß: den Median
- Was ist der Median?
- Berechnung: allgemein Infos
- Ausrechnen bei gerader Stichprobe
- Ausrechnen bei ungerader Stichprobe
Es ist hilfreich, wenn Ihr euch bereits mit Skalenniveaus auskennt.
Was ist der Median?
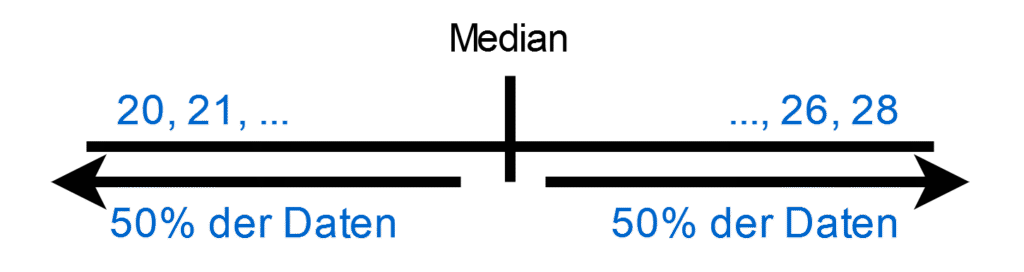
Der Median ist der mittlere Wert einer geordneten Datenreihe. Er teilt die Daten in zwei gleich große Hälften: D.h. 50 % der Werte liegen unterhalb des Medians und 50 % der Werte liegen oberhalb des Medians.
Der Median kann bereits ab der Ordinalskala berechnet werden (anders als der Mittelwert) und ist ideal für rangbasierte Daten (z. B. Schulnoten, Kundenzufriedenheitsskalen).
Berechnung
Betrachten wir den Median anhand eines Beispiels.
Stellt euch vor, ihr habt das Alter von zehn Personen gegeben und wollt den Median dieser Stichprobe ausrechnen: Zuerst ordnet ihr die Zahlen der Reihe nach:
$$ 20, 21, 22, 22, 22, 24, 25, 25, 26, 28 $$
Und das hier ist die Formel für die Berechnung des Medians:
$$\widetilde{x}_{0.5} = \begin{cases} x_{\frac{n+1}{2}} & \text{falls } n \text{ ungerade} \\ \frac{1}{2} \left( x_{\frac{n}{2}} + x_{\frac{n}{2}+1} \right) & \text{falls } n \text{ gerade}
\end{cases}$$
Hier bezeichnet „n“ den Stichprobenumfang und es kann angemerkt werden, dass es für den Median übrigens keine keine einheitliche Notation gibt, also nicht wundern, wenn bei euch ein anderes Zeichen für diesen Lageparameter verwendet wird.
In Worten zusammengefasst bedeutet diese Formel, dass bei einer ungeraden Stickprobe der Median den Wert annimmt, der genau in der Mitte der Stichprobe liegt. Das ist genau der Wert, der an der Stelle \(\frac{n+1}{2}\). Bei einer geraden Stichprobe wird der Median aus dem arithmetischen Mittel der beiden mittleren Werte berechnet.
Beispiel mit gerader Stichprobe
In unserem Beispiel haben wir 10 Werte. Das heißt, es handelt sich also um einen geraden Stichprobenumfang und wir nehmen die untere der beiden Formeln mit n = 10.
$$ \begin{align*}\widetilde{x}_{0.5} &= \frac{1}{2} \left( x_{\frac{n}{2}} + x_{\frac{n}{2}+1}\right) \\ \widetilde{x}_{0.5} &= \frac{1}{2} \left( x_{5} + x_{6}\right)\end{align*}$$
\(x_5\) und \(x_6\) bedeuten jetzt natürlich nicht, dass ihr 5 und 6 addieren sollt, sondern damit sind der fünfte und sechste Wert unserer geordneten Datenreihe gemeint.
Das heißt, ihr müsst nur abzählen, welche Werte an fünfter und sechster Stelle liegen und die entsprechenden Zahlen einsetzen.
Die Werte durchzunummerieren, vereinfacht euch das Ganze.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 20 | 21 | 22 | 22 | 22 | 24 | 25 | 25 | 26 | 28 |
\(x_5\) und \(x_6\) enstprechen also den Werten 22 und 24.
$$\widetilde{x}_{0.5} = \frac{1}{2} \left( 22 + 24\right) = 23$$
Wir erhalten als Median 23 Jahre. Das bedeutet, dass 50% der Gruppe jünger als 23 und 50% der Gruppe älter als 23 Jahre sind.
Auch ohne die Formel kann man leicht sehen, dass der Median das Mittel aus 22 und 24 ist, da das die beiden Werte sind, die in der Mitte liegen.
Berechnung mit ungerader Stichprobe
Wenn wir unserer Stichprobe noch einen Wert hinzufügen, bekommen wir einen ungeraden Stichprobenumfang. Also fügen wir noch eine Person hinzu, die 30 Jahre alt ist. Damit haben wir n = 11 Werte.
20, 21, 22, 22, 22, 24, 25, 25, 26, 28, 30
Hier kann man den Median auf einen Blick erkennen. Und zwar ist er 24, weil dieser Wert genau in der Mitte liegt.
Wollen wir die Formel verwenden, nehmen wir jetzt die obere der beiden, also \(\widetilde{x}_{0.5} = x_{\frac{n+1}{2}} \)
Die Berechnung ist beinahe dieselbe. Da wir nun einen Wert mehr haben, setzen wir nur für n = 11 ein. Somit erhalten wir:
$$\begin{align*}\widetilde{x}_{0.5} &= x_{\frac{11+1}{2}}\\ \widetilde{x}_{0.5} &= x_{\frac{12}{2}}\\ \widetilde{x}_{0.5} &= x_{6}\\ \widetilde{x}_{0.5} &= 24\end{align*}$$
Das bedeutet, der Median ist nun der 6. Wert der geordneten Daten, also 24 Jahre. In diesem Fall bedeutet dies, dass die Hälfte der Gruppe jünger als 24 und die andere Hälfte älter als 24 Jahre ist.
Median
Hier betrachten wir ein weiteres Lagemaß: den Median
- Was ist der Median?
- Berechnung: allgemein Infos
- Ausrechnen bei gerader Stichprobe
- Ausrechnen bei ungerader Stichprobe
Es ist hilfreich, wenn Ihr euch bereits mit Skalenniveaus auskennt.
Was ist der Median?
Der Median ist der mittlere Wert einer geordneten Datenreihe. Er teilt die Daten in zwei gleich große Hälften: D.h. 50 % der Werte liegen unterhalb des Medians und 50 % der Werte liegen oberhalb des Medians.
Der Median kann bereits ab der Ordinalskala berechnet werden (anders als der Mittelwert) und ist ideal für rangbasierte Daten (z. B. Schulnoten, Kundenzufriedenheitsskalen).

Berechnung
Betrachten wir den Median anhand eines Beispiels.
Stellt euch vor, ihr habt das Alter von zehn Personen gegeben und wollt den Median dieser Stichprobe ausrechnen: Zuerst ordnet ihr die Zahlen der Reihe nach:
$$ 20, 21, 22, 22, 22, 24, 25, 25, 26, 28 $$
Und das hier ist die Formel für die Berechnung des Medians:
$$\widetilde{x}_{0.5} = \begin{cases} x_{\frac{n+1}{2}} & \text{falls } n \text{ ungerade} \\ \frac{1}{2} \left( x_{\frac{n}{2}} + x_{\frac{n}{2}+1} \right) & \text{falls } n \text{ gerade}
\end{cases}$$
Hier bezeichnet „n“ den Stichprobenumfang und es kann angemerkt werden, dass es für den Median übrigens keine keine einheitliche Notation gibt, also nicht wundern, wenn bei euch ein anderes Zeichen für diesen Lageparameter verwendet wird.
In Worten zusammengefasst bedeutet diese Formel, dass bei einer ungeraden Stickprobe der Median den Wert annimmt, der genau in der Mitte der Stichprobe liegt. Das ist genau der Wert, der an der Stelle \(\frac{n+1}{2}\). Bei einer geraden Stichprobe wird der Median aus dem arithmetischen Mittel der beiden mittleren Werte berechnet.
Beispiel mit gerader Stichprobe
In unserem Beispiel haben wir 10 Werte. Das heißt, es handelt sich also um einen geraden Stichprobenumfang und wir nehmen die untere der beiden Formeln mit n = 10.
$$ \begin{align*}\widetilde{x}_{0.5} &= \frac{1}{2} \left( x_{\frac{n}{2}} + x_{\frac{n}{2}+1}\right) \\ \widetilde{x}_{0.5} &= \frac{1}{2} \left( x_{5} + x_{6}\right)\end{align*}$$
\(x_5\) und \(x_6\) bedeuten jetzt natürlich nicht, dass ihr 5 und 6 addieren sollt, sondern damit sind der fünfte und sechste Wert unserer geordneten Datenreihe gemeint.
Das heißt, ihr müsst nur abzählen, welche Werte an fünfter und sechster Stelle liegen und die entsprechenden Zahlen einsetzen.
Die Werte durchzunummerieren, vereinfacht euch das Ganze.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 20 | 21 | 22 | 22 | 22 | 24 | 25 | 25 | 26 | 28 |
\(x_5\) und \(x_6\) enstprechen also den Werten 22 und 24.
$$\widetilde{x}_{0.5} = \frac{1}{2} \left( 22 + 24\right) = 23$$
Wir erhalten als Median 23 Jahre. Das bedeutet, dass 50% der Gruppe jünger als 23 und 50% der Gruppe älter als 23 Jahre sind.
Auch ohne die Formel kann man leicht sehen, dass der Median das Mittel aus 22 und 24 ist, da das die beiden Werte sind, die in der Mitte liegen.
Berechnung mit ungerader Stichprobe
Wenn wir unserer Stichprobe noch einen Wert hinzufügen, bekommen wir einen ungeraden Stichprobenumfang. Also fügen wir noch eine Person hinzu, die 30 Jahre alt ist. Damit haben wir n = 11 Werte.
20, 21, 22, 22, 22, 24, 25, 25, 26, 28, 30
Hier kann man den Median auf einen Blick erkennen. Und zwar ist er 24, weil dieser Wert genau in der Mitte liegt.
Wollen wir die Formel verwenden, nehmen wir jetzt die obere der beiden, also \(\widetilde{x}_{0.5} = x_{\frac{n+1}{2}} \)
Die Berechnung ist beinahe dieselbe. Da wir nun einen Wert mehr haben, setzen wir nur für n = 11 ein. Somit erhalten wir:
$$\begin{align*}\widetilde{x}_{0.5} &= x_{\frac{11+1}{2}}\\ \widetilde{x}_{0.5} &= x_{\frac{12}{2}}\\ \widetilde{x}_{0.5} &= x_{6}\\ \widetilde{x}_{0.5} &= 24\end{align*}$$
Das bedeutet, der Median ist nun der 6. Wert der geordneten Daten, also 24 Jahre. In diesem Fall bedeutet dies, dass die Hälfte der Gruppe jünger als 24 und die andere Hälfte älter als 24 Jahre ist.
