Tauche ein in unsere modebewusste Statistik-Welt.
Pearson-Korrelationskoeffizient
- Eigenschaften
- Interpretation
- Berechnung per Hand
- Korrelation und Kausalität
- linearer Zusammenhang
Für dieses Thema ist es hilfreich, wenn ihr bereits über die Standardabweichung und Kovarianz Bescheid wisst.
Informationen zum Korrelationskoeffizienten
Der Pearson-Korrelationskoeffizient wird auch als Produkt-Moment Korrelation bezeichnet und beschreibt den linearen Zusammenhang zwischen zwei Variablen. Die Variablen müssen mindestens intervallskaliert und normalverteilt sein und sollten keine Ausreißer beinhalten.
Er kann Werte zwischen -1 und 1 annehmen und wird in der Regel mit \(r_{xy}\) gekennzeichnet.
$$ -1 \leq r_{xy} \leq 1$$
Je näher der Korrelationskoeffizient bei – 1 oder + 1 liegt, desto stärker ist der Zusammenhang. Das bedeutet wiederum natürlich je näher bei null, desto schwächer der Zusammenhang.
Zur Bestimmung der Höhe des Zusammenhangs gibt es zahlreiche Ansätze. Wir verwenden hier die Interpretation nach Cohen:
$$\begin{align}|r_{xy}| &= 0.1 \rightarrow \text{schwache Korrelation}\\ |r_{xy}| &= 0.3 \rightarrow \text{mittlere Korrelation}\\ |r_{xy}| &= 0.5 \rightarrow \text{starke Korrelation}\end{align}$$
Wichtig ist hier, dass ein Minus keine Auswirkung auf die Höhe des Zusammenhangs hat. Eine Korrelation von +0,5 ist genauso stark wie eine Korrelation von – 0,5.
Ab wann ein Korrelationskoeffizient als hoch, mittel oder niedrig eingestuft werden kann, wird sehr unterschiedlich beurteilt. Andere Quellen verwenden andere Richtwerte oder mehr als 3 Abstufungen. Die Interpretation nach Cohen soll euch einfach einen ersten Anhaltspunkt geben.
Neben der Höhe kann auch die Richtung des Zusammenhangs bestimmt werden. Dies geschieht anhand des Vorzeichens. Ein Plus bedeutet dabei eine positive, ein Minus eine negative Korrelation.
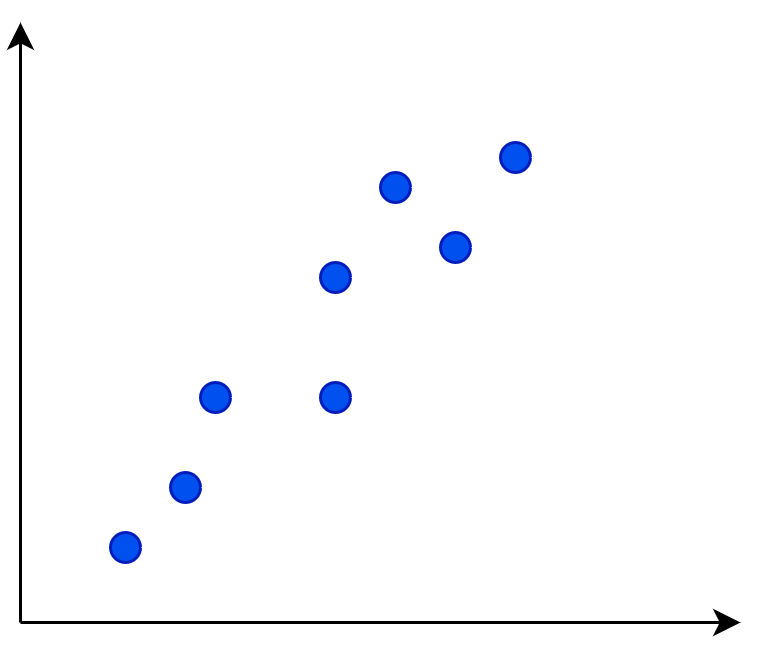
Ein positiver Zusammenhang bedeutet einfach gesagt: je mehr, desto mehr. Sprich, wenn das eine Merkmal steigt, steigt auch das Andere. Ein Beispiel dafür wäre, je größer eine Person, desto schwerer ist sie.
Ein negativer Zusammenhang bedeutet, je mehr, desto weniger. Wenn das eine Merkmal steigt, fällt das Andere. Ein Beispiel dafür wäre, je höher das Wirtschaftswachstum, desto niedriger die Arbeitslosenquote.
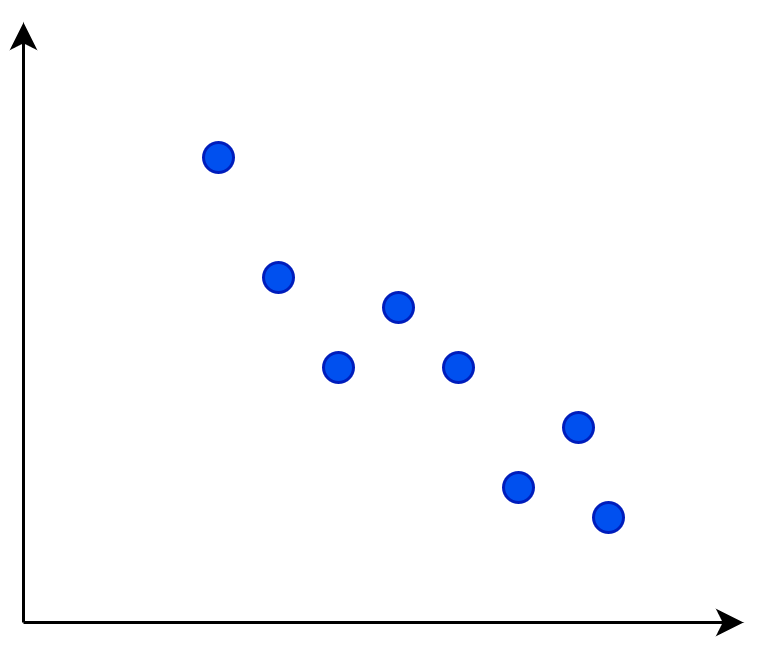
Wie ihr hier seht, sind Streudiagramme, auch Punktewolke oder auf Englisch Scatterplot genannt, ein gutes Werkzeug, um die Korrelation zu betrachten. Sie stellen den Zusammenhang zwischen zwei metrischen Variablen grafisch dar und die Richtung und die Stärke des Zusammenhangs lässt sich gut feststellen oder zumindest abschätzen. Die Richtung kann man daran erkennen, ob die Punkte steigen oder fallen und je näher die Punkte auf einer gedachten Geraden liegen, desto höher ist der Zusammenhang.
Formel des Korrelationskoeffizienten
Schauen wir uns die Formel für den Korrelationskoeffizienten an. Sie ist in ihrer eigentlichen Form sehr simpel. Man dividiert einfach nur die Kovarianz von X und Y (\(s_{xy}\)) durch die Standardabweichung von X (\(s_{x}\)) Mal der Standardabweichung von Y (\(s_{y}\)) :
$$r_{xy} = \frac{s_{xy}}{s_x * s_y}$$
Wenn wir die Definitionen der Kovarianz und Standardabweichung einsetzten, kommen wir auf:
$$r_{xy} = \frac{\sum_{i=1}^n(x_i – \bar{x})(y_i – \bar{y})}{\sqrt{\sum_{i=1}^n(x_i – \bar{x})^2} * \sqrt{\sum_{i=1}^n(y_i – \bar{y})^2}}$$
Ähnlich wie bei der Formel für die Varianz, ist diese Formel einfacher herzuleiten, jedoch ist sie zum Rechnen nicht optimal. Einerseits da man in der Regel länger braucht und andererseits, weil auch die Gefahr von Rundungsfehlern besteht. Dieser Umstand wird im Beitrag zur Varianz genauer beschrieben.
Es gibt auch hier eine rechentechnisch günstigere Version der Formel!
$$r_{xy} = \frac{\sum_{i=1}^n x_i y_i – n\bar{x}\bar{y}}{\sqrt{\sum_{i=1}^n x_i^2 -n\bar{x}^2 }*\sqrt{\sum_{i=1}^n y_i^2 – n\bar{y}^2 }}$$
Das sieht jetzt alles anfangs sehr kompliziert aus, aber wir werden das jetzt Schritt für Schritt durchgehen und ihr werdet sehen, dass es gar nicht so schlimm ist wie es aussieht.
Mit dieser Formel seid ihr generell schneller. Ihr spart euch also viel Zeit und zusätzlich habt ihr nicht das Problem von Rundungsfehlern.
Man muss hier natürlich sagen, dass die beiden Formel völlig äquivalent sind! Man kann die Terme in der ersten Formel umformen, um auf die zweite Formel zu kommen. Wenn ihr eure Matheskills üben wollt, könnt ihr das ja mal probieren.
Berechnung anhand eines Beispiels
| Rechnung (\(x_i\)) | Trinkgeld (\(y_i\)) |
| 23 | 2 |
| 39 | 4 |
| 26 | 3 |
| 35 | 5 |
| 52 | 6 |
Für die Berechnung des Korrelationskoeffizienten verwenden wir das Beispiel eines Kellners, der den Zusammenhang zwischen der Höhe des Rechnungsbetrages und der Höhe des Trinkgeldes berechnen möchte. Dazu hat er 5 Rechnungsbeträge gesammelt und sich das jeweilige Trinkgeld dazu notiert.
Um die 3 Summen zu berechnen, die in der Formel vorkommen, fügen wir eine Spalte für jede Summe der Tabelle hinzu. Diese Spalten sind \(x_i*y_i \quad x_i^2 \quad y_i^2\).
Dann rechnen wir die Werte dieser Spalten mithilfe der gegebenen x und y Werte aus. Das ist ziemlich selbsterklärend. In der Spalte (\(x_i * y_i\)) rechnet man für i=1: 23 *2. In der Spalte (\(x_i^2\)) rechnet man für i=1: 23^2. In der Spalte (\(y_i^2\)) rechnet man für i=1: 2^2 usw.
| (\(x_i\)) | (\(y_i\)) | (\(x_i * y_i\)) | (\(x_i^2\)) | (\(y_i^2\)) |
| 23 | 2 | 46 | 529 | 4 |
| 39 | 4 | 156 | 1521 | 16 |
| 26 | 3 | 78 | 676 | 9 |
| 35 | 5 | 175 | 1225 | 25 |
| 52 | 6 | 312 | 2704 | 36 |
Jetzt können wir ganz einfach die gewollten Summen berechnen.
| \(\sum\)175 | \(\sum\)20 | \(\sum\)767 | \(\sum\)6655 | \(\sum\)90 |
Schlussendlich benötigen wir noch den Mittelwert von X und Y. Hier dividieren wir einfach die Summe der Spalten \(x_i\) und \(y_i\) durch die Anzahl der Datenpunkte. Die Anzahl n ist 5, da wir 5 Datenpaare haben.
$$\begin{align}n &= 5\\ \bar{x} &= \frac{175}{5} = 35\\ \bar{y} &= \frac{20}{5} = 4 \end{align}$$
Jetzt haben wir alle Werte und können sie in die Formel einsetzen:
$$\begin{align}r_{xy} &= \frac{\sum_{i=1}^n x_i y_i – n\bar{x}\bar{y}}{\sqrt{\sum_{i=1}^n x_i^2 -n\bar{x}^2 }*\sqrt{\sum_{i=1}^n y_i^2 – n\bar{y}^2 }}\\ r_{xy} &= \frac{767- 5*35*4}{\sqrt{6655 -5*35^2 }*\sqrt{90 – 5*4^2 }}\\ r_{xy} &= \frac{67}{72.8}\\ r_{xy} &= 0.92\end{align}$$
Nach der vorher behandelten Interpretation handelt es sich hier um eine positive, starke Korrelation.
Korrelation und Kausalität
Ein wichtiger Punkt, wenn man mit Korrelationen arbeitet und welcher von vielen oft missverstanden wird, ist, dass eine bestehende Korrelation zwischen 2 Variablen nicht automatisch einen kausalen Zusammenhang impliziert.
Korrelation \(\neq\) Kausalität
Als Kausalität versteht man die Beziehung zwischen Ursache und Wirkung.
Nur weil 2 Variablen korrelieren, heißt das nicht, dass eine Variable die andere beeinflusst.
Sehen wir uns dafür ein einfaches Beispiel an.
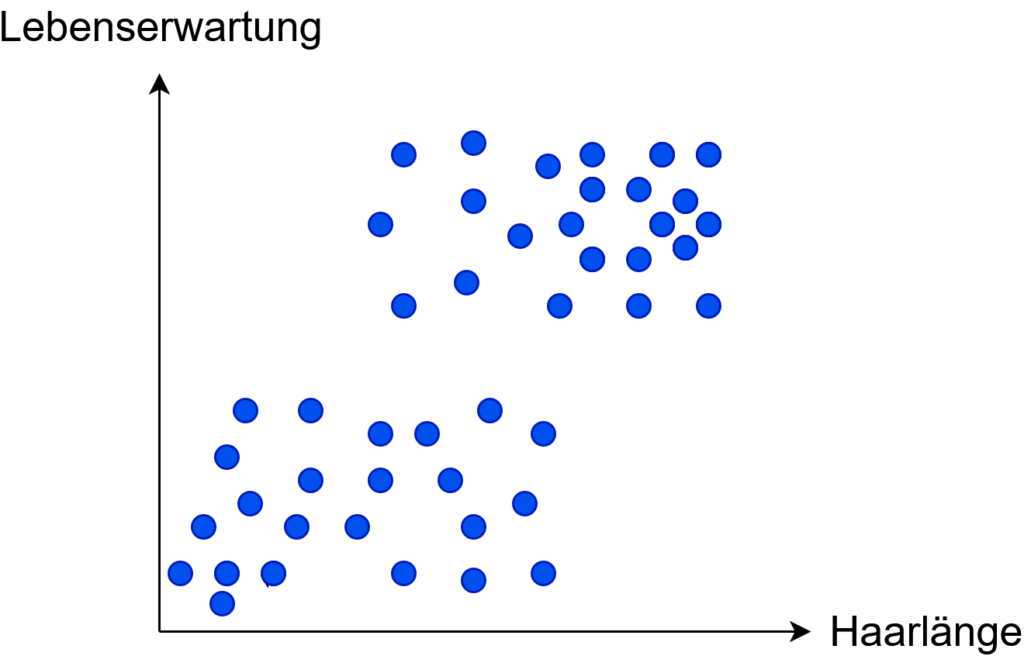
Hier haben wir ein Streudiagramm zwischen der Haarlänge von Personen und deren Lebenserwartung. Wir können hier eine positive Korrelation erkennen (wenn die Haarlänge ansteigt, erhöht sich auch die Lebenserwartung).
Heißt das nun also, dass ich mit längeren Haaren länger leben würde?
Natürlich nicht, sonst hätten wir ja alle lange Haare. Und genau das ist der Punkt, wo ihr bei Korrelationen aufpassen müsst. Nur weil wir einen Zusammenhang zwischen diesen beiden Variablen gefunden haben, heißt das noch lange nicht, dass sich die Haarlänge auf die Lebensdauer auswirkt.
Der Grund, warum wir hier eine positive Korrelation gefunden haben, ist ganz einfach. Und zwar gibt es noch eine dritte Variable, die beide beeinflusst. Und zwar das Geschlecht. Frauen haben in der Regel längere Haare als Männer und sie haben in der Regel auch eine höhere Lebenserwartung.
Kontrollieren wir nach Geschlecht, können wir sehr schnell erkennen, dass weder bei Frauen noch bei Männern sich die Haarlänge auf die Lebenserwartung auswirkt.
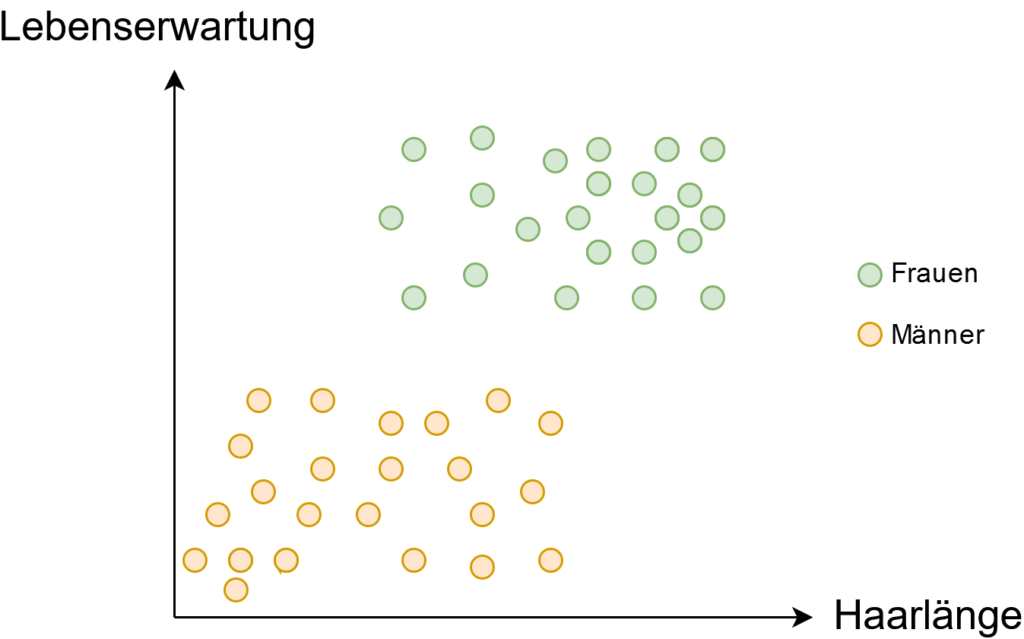
In vielen Fällen, gibt es weitere Faktoren, oft auch Drittvariablen genannt, die die korrelierenden Variablen beeinflussen. So wie in unserem Beispiel das Geschlecht. Also Vorsicht mit vorschnellen Schlussfolgerungen bei Korrelationen.
Linearer Zusammenhang
Wir haben bereits zu Beginn erwähnt, dass es sich hierbei um den LINEAREN Zusammenhang zwischen zwei Variablen handelt. Das heißt, wenn wir einen Korrelationskoeffizienten von 0 errechnen, heißt es nicht automatisch, dass kein Zusammenhang zwischen den Variablen besteht.
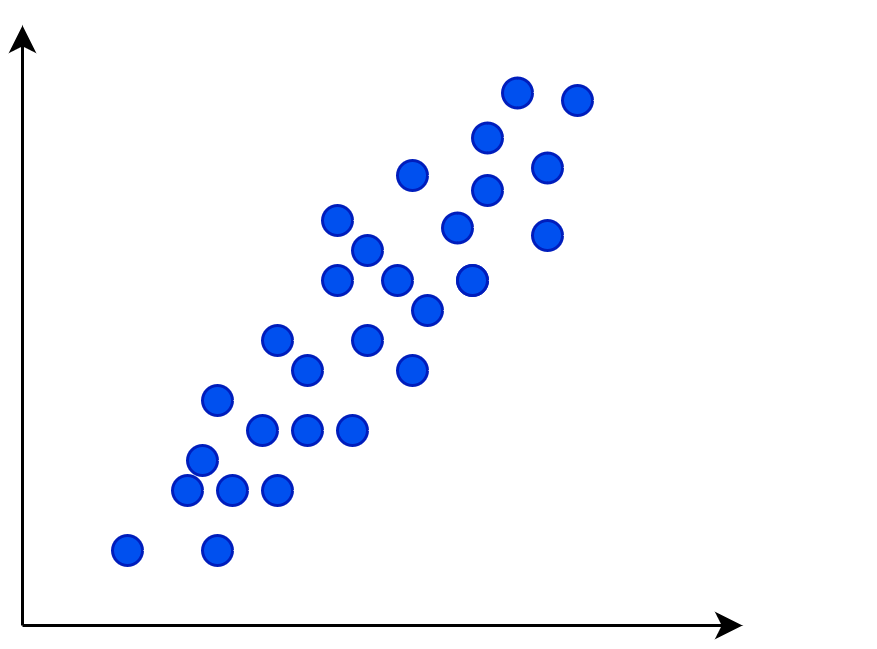
Dieses Beispiel hat einen Korrelationskoeffizienten von ca. 0,95.
D.h. wir haben eindeutig einen Zusammenhang zwischen den beiden Variablen.
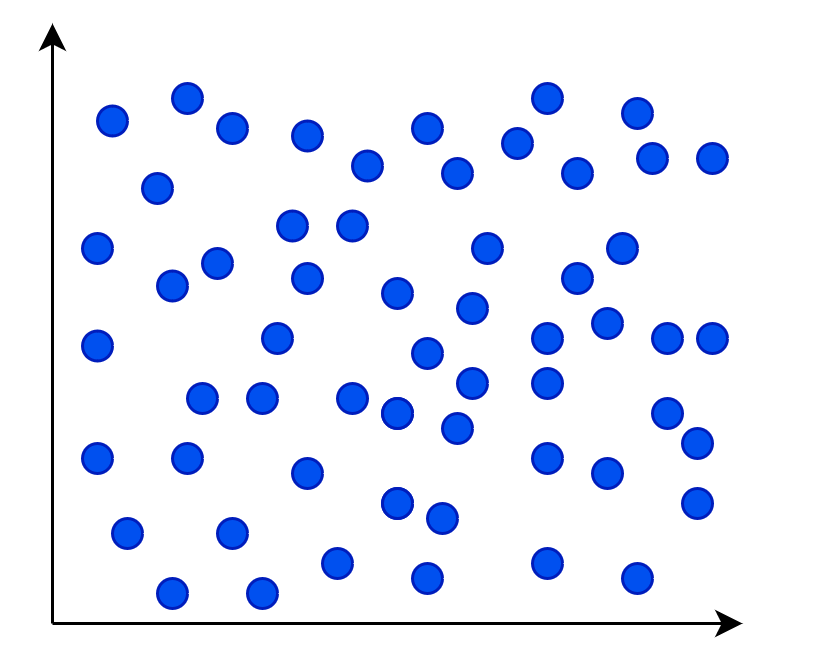
In diesem zweiten Beispiel haben wir einen Korrelationskoeffizienten von 0 und anhand des Streudiagramms können wir erkennen, dass hier überhaupt kein Zusammenhang zwischen den Variablen besteht, da die Punkte wild streuen.
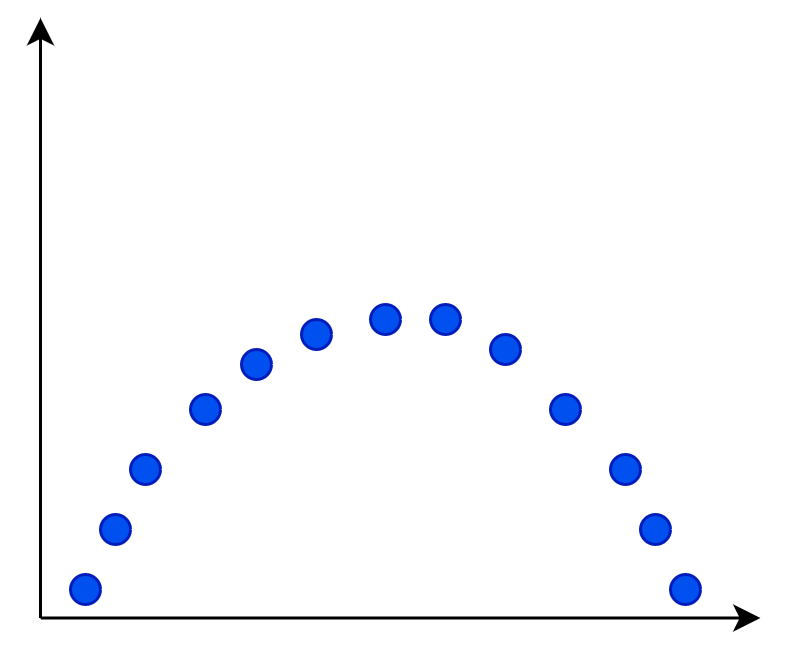
In diesem letzten Beispiel haben wir wieder einen Korrelationskoeffizienten von 0, jedoch haben wir hier einen Zusammenhang zwischen den Variablen. Wir können anhand des Streudiagramms klar erkennen, dass die Punkte eindeutig einem Muster folgen.
Warum ist dann der Korrelationskoeffizient hier Null?
Weil der Korrelationskoeffizient nur die Stärke eines LINEAREN Zusammenhangs ermittelt. Man kann hier schlecht eine Gerade durch die Punkte durchziehen.
Das heißt ein Korrelationskoeffizient von 0 bedeutet nicht zwingend, dass kein Zusammenhang zwischen den Variablen besteht, sondern nur, dass es keinen linearen Zusammenhang zwischen den Variablen gibt.
Pearson-Korrelationskoeffizient
- Eigenschaften
- Interpretation
- Berechnung per Hand
- Korrelation und Kausalität
- linearer Zusammenhang
Für dieses Thema ist es hilfreich, wenn ihr bereits über die Standardabweichung und Kovarianz Bescheid wisst.
Informationen zum Korrelationskoeffizienten
Der Pearson-Korrelationskoeffizient wird auch als Produkt-Moment Korrelation bezeichnet und beschreibt den linearen Zusammenhang zwischen zwei Variablen. Die Variablen müssen mindestens intervallskaliert und normalverteilt sein und sollten keine Ausreißer beinhalten.
Er kann Werte zwischen -1 und 1 annehmen und wird in der Regel mit \(r_{xy}\) gekennzeichnet.
$$ -1 \leq r_{xy} \leq 1$$
Je näher der Korrelationskoeffizient bei – 1 oder + 1 liegt, desto stärker ist der Zusammenhang. Das bedeutet wiederum natürlich je näher bei null, desto schwächer der Zusammenhang.
Zur Bestimmung der Höhe des Zusammenhangs gibt es zahlreiche Ansätze. Wir verwenden hier die Interpretation nach Cohen:
$$\begin{align}|r_{xy}| &= 0.1 \rightarrow \text{schwache Korrelation}\\ |r_{xy}| &= 0.3 \rightarrow \text{mittlere Korrelation}\\ |r_{xy}| &= 0.5 \rightarrow \text{starke Korrelation}\end{align}$$
Wichtig ist hier, dass ein Minus keine Auswirkung auf die Höhe des Zusammenhangs hat. Eine Korrelation von +0,5 ist genauso stark wie eine Korrelation von – 0,5.
Ab wann ein Korrelationskoeffizient als hoch, mittel oder niedrig eingestuft werden kann, wird sehr unterschiedlich beurteilt. Andere Quellen verwenden andere Richtwerte oder mehr als 3 Abstufungen. Die Interpretation nach Cohen soll euch einfach einen ersten Anhaltspunkt geben.
Neben der Höhe kann auch die Richtung des Zusammenhangs bestimmt werden. Dies geschieht anhand des Vorzeichens. Ein Plus bedeutet dabei eine positive, ein Minus eine negative Korrelation.

Ein positiver Zusammenhang bedeutet einfach gesagt: je mehr, desto mehr. Sprich, wenn das eine Merkmal steigt, steigt auch das Andere. Ein Beispiel dafür wäre, je größer eine Person, desto schwerer ist sie.
Ein negativer Zusammenhang bedeutet, je mehr, desto weniger. Wenn das eine Merkmal steigt, fällt das Andere. Ein Beispiel dafür wäre, je höher das Wirtschaftswachstum, desto niedriger die Arbeitslosenquote.

Wie ihr hier seht, sind Streudiagramme, auch Punktewolke oder auf Englisch Scatterplot genannt, ein gutes Werkzeug, um die Korrelation zu betrachten. Sie stellen den Zusammenhang zwischen zwei metrischen Variablen grafisch dar und die Richtung und die Stärke des Zusammenhangs lässt sich gut feststellen oder zumindest abschätzen. Die Richtung kann man daran erkennen, ob die Punkte steigen oder fallen und je näher die Punkte auf einer gedachten Geraden liegen, desto höher ist der Zusammenhang.
Formel des Korrelationskoeffizienten
Schauen wir uns die Formel für den Korrelationskoeffizienten an. Sie ist in ihrer eigentlichen Form sehr simpel. Man dividiert einfach nur die Kovarianz von X und Y (\(s_{xy}\)) durch die Standardabweichung von X (\(s_{x}\)) Mal der Standardabweichung von Y (\(s_{y}\)) :
$$r_{xy} = \frac{s_{xy}}{s_x * s_y}$$
Wenn wir die Definitionen der Kovarianz und Standardabweichung einsetzten, kommen wir auf:
$$r_{xy} = \frac{\sum_{i=1}^n(x_i – \bar{x})(y_i – \bar{y})}{\sqrt{\sum_{i=1}^n(x_i – \bar{x})^2} * \sqrt{\sum_{i=1}^n(y_i – \bar{y})^2}}$$
Ähnlich wie bei der Formel für die Varianz, ist diese Formel einfacher herzuleiten, jedoch ist sie zum Rechnen nicht optimal. Einerseits da man in der Regel länger braucht und andererseits, weil auch die Gefahr von Rundungsfehlern besteht. Dieser Umstand wird im Beitrag zur Varianz genauer beschrieben.
Es gibt auch hier eine rechentechnisch günstigere Version der Formel!
$$r_{xy} = \frac{\sum_{i=1}^n x_i y_i – n\bar{x}\bar{y}}{\sqrt{\sum_{i=1}^n x_i^2 -n\bar{x}^2 }*\sqrt{\sum_{i=1}^n y_i^2 – n\bar{y}^2 }}$$
Das sieht jetzt alles anfangs sehr kompliziert aus, aber wir werden das jetzt Schritt für Schritt durchgehen und ihr werdet sehen, dass es gar nicht so schlimm ist wie es aussieht.
Mit dieser Formel seid ihr generell schneller. Ihr spart euch also viel Zeit und zusätzlich habt ihr nicht das Problem von Rundungsfehlern.
Man muss hier natürlich sagen, dass die beiden Formel völlig äquivalent sind! Man kann die Terme in der ersten Formel umformen, um auf die zweite Formel zu kommen. Wenn ihr eure Matheskills üben wollt, könnt ihr das ja mal probieren.
Berechnung anhand eines Beispiels
| Rechnung (\(x_i\)) | Trinkgeld (\(y_i\)) |
| 23 | 2 |
| 39 | 4 |
| 26 | 3 |
| 35 | 5 |
| 52 | 6 |
Für die Berechnung des Korrelationskoeffizienten verwenden wir das Beispiel eines Kellners, der den Zusammenhang zwischen der Höhe des Rechnungsbetrages und der Höhe des Trinkgeldes berechnen möchte. Dazu hat er 5 Rechnungsbeträge gesammelt und sich das jeweilige Trinkgeld dazu notiert.
Um die 3 Summen zu berechnen, die in der Formel vorkommen, fügen wir eine Spalte für jede Summe der Tabelle hinzu. Diese Spalten sind \(x_i*y_i \quad x_i^2 \quad y_i^2\).
Dann rechnen wir die Werte dieser Spalten mithilfe der gegebenen x und y Werte aus. Das ist ziemlich selbsterklärend. In der Spalte (\(x_i * y_i\)) rechnet man für i=1: 23 *2. In der Spalte (\(x_i^2\)) rechnet man für i=1: 23^2. In der Spalte (\(y_i^2\)) rechnet man für i=1: 2^2 usw.
| (\(x_i\)) | (\(y_i\)) | (\(x_i * y_i\)) | (\(x_i^2\)) | (\(y_i^2\)) |
| 23 | 2 | 46 | 529 | 4 |
| 39 | 4 | 156 | 1521 | 16 |
| 26 | 3 | 78 | 676 | 9 |
| 35 | 5 | 175 | 1225 | 25 |
| 52 | 6 | 312 | 2704 | 36 |
Jetzt können wir ganz einfach die gewollten Summen berechnen.
| \(\sum\)175 | \(\sum\)20 | \(\sum\)767 | \(\sum\)6655 | \(\sum\)90 |
Schlussendlich benötigen wir noch den Mittelwert von X und Y. Hier dividieren wir einfach die Summe der Spalten \(x_i\) und \(y_i\) durch die Anzahl der Datenpunkte. Die Anzahl n ist 5, da wir 5 Datenpaare haben.
$$\begin{align}n &= 5\\ \bar{x} &= \frac{175}{5} = 35\\ \bar{y} &= \frac{20}{5} = 4 \end{align}$$
Jetzt haben wir alle Werte und können sie in die Formel einsetzen:
$$\begin{align}r_{xy} &= \frac{\sum_{i=1}^n x_i y_i – n\bar{x}\bar{y}}{\sqrt{\sum_{i=1}^n x_i^2 -n\bar{x}^2 }*\sqrt{\sum_{i=1}^n y_i^2 – n\bar{y}^2 }}\\ r_{xy} &= \frac{767- 5*35*4}{\sqrt{6655 -5*35^2 }*\sqrt{90 – 5*4^2 }}\\ r_{xy} &= \frac{67}{72.8}\\ r_{xy} &= 0.92\end{align}$$
Nach der vorher behandelten Interpretation handelt es sich hier um eine positive, starke Korrelation.
Korrelation und Kausalität
Ein wichtiger Punkt, wenn man mit Korrelationen arbeitet und welcher von vielen oft missverstanden wird, ist, dass eine bestehende Korrelation zwischen 2 Variablen nicht automatisch einen kausalen Zusammenhang impliziert.
Korrelation \(\neq\) Kausalität
Als Kausalität versteht man die Beziehung zwischen Ursache und Wirkung.
Nur weil 2 Variablen korrelieren, heißt das nicht, dass eine Variable die andere beeinflusst.
Sehen wir uns dafür ein einfaches Beispiel an.

Hier haben wir ein Streudiagramm zwischen der Haarlänge von Personen und deren Lebenserwartung. Wir können hier eine positive Korrelation erkennen (wenn die Haarlänge ansteigt, erhöht sich auch die Lebenserwartung).
Heißt das nun also, dass ich mit längeren Haaren länger leben würde?
Natürlich nicht, sonst hätten wir ja alle lange Haare. Und genau das ist der Punkt, wo ihr bei Korrelationen aufpassen müsst. Nur weil wir einen Zusammenhang zwischen diesen beiden Variablen gefunden haben, heißt das noch lange nicht, dass sich die Haarlänge auf die Lebensdauer auswirkt.
Der Grund, warum wir hier eine positive Korrelation gefunden haben, ist ganz einfach. Und zwar gibt es noch eine dritte Variable, die beide beeinflusst. Und zwar das Geschlecht. Frauen haben in der Regel längere Haare als Männer und sie haben in der Regel auch eine höhere Lebenserwartung.
Kontrollieren wir nach Geschlecht, können wir sehr schnell erkennen, dass weder bei Frauen noch bei Männern sich die Haarlänge auf die Lebenserwartung auswirkt.

In vielen Fällen, gibt es weitere Faktoren, oft auch Drittvariablen genannt, die die korrelierenden Variablen beeinflussen. So wie in unserem Beispiel das Geschlecht. Also Vorsicht mit vorschnellen Schlussfolgerungen bei Korrelationen.
Linearer Zusammenhang
Wir haben bereits zu Beginn erwähnt, dass es sich hierbei um den LINEAREN Zusammenhang zwischen zwei Variablen handelt. Das heißt, wenn wir einen Korrelationskoeffizienten von 0 errechnen, heißt es nicht automatisch, dass kein Zusammenhang zwischen den Variablen besteht.

Dieses Beispiel hat einen Korrelationskoeffizienten von ca. 0,95.
D.h. wir haben eindeutig einen Zusammenhang zwischen den beiden Variablen.

In diesem zweiten Beispiel haben wir einen Korrelationskoeffizienten von 0 und anhand des Streudiagramms können wir erkennen, dass hier überhaupt kein Zusammenhang zwischen den Variablen besteht, da die Punkte wild streuen.

In diesem letzten Beispiel haben wir wieder einen Korrelationskoeffizienten von 0, jedoch haben wir hier einen Zusammenhang zwischen den Variablen. Wir können anhand des Streudiagramms klar erkennen, dass die Punkte eindeutig einem Muster folgen.
Warum ist dann der Korrelationskoeffizient hier Null?
Weil der Korrelationskoeffizient nur die Stärke eines LINEAREN Zusammenhangs ermittelt. Man kann hier schlecht eine Gerade durch die Punkte durchziehen.
Das heißt ein Korrelationskoeffizient von 0 bedeutet nicht zwingend, dass kein Zusammenhang zwischen den Variablen besteht, sondern nur, dass es keinen linearen Zusammenhang zwischen den Variablen gibt.
