Tauche ein in unsere modebewusste Statistik-Welt.
Schiefe – Erklärung
Heute geht es um die Schiefe.
- Wichtige Infos
- Schiefe anhand von Häufigkeitsverteilung
- Schiefe anhand von Boxplot
- Fechner’sche Lageregel
- Berechnungen (Quartils- und Momentschiefe)
Wichtiges Vorwissen zu diesem Beitrag sind die Lagemaße.
Außerdem ist es hilfreich, wenn ihr auch schon wisst was Boxplots sind und wie man die Standardabweichung berechnet.
Infos
Die Schiefe beschreibt die Stärke der Asymmetrie einer Verteilung und wird auf Englisch Skewness genannt. Eine symmetrische Verteilung hat eine Schiefe von Null. Falls sie nicht symmetrisch ist, wird sie als schief bezeichnet, wobei generell zwischen rechts- und linksschief unterschieden wird. Die Schiefe ist im Allgemeinen nicht normiert, sie kann also beliebig große Werte annehmen.
Es gibt viele verschiedene Ansätze zur Bestimmung der Schiefe, in diesem Video sehen wir uns die Fechner‘sche Lageregel, die Quartilsschiefe, die Person-Schiefemaße und die Momentschiefe an. Dabei gibt es zu allen Varianten eine kurze Erklärung und wie man diese berechnet.
Rechtsschief
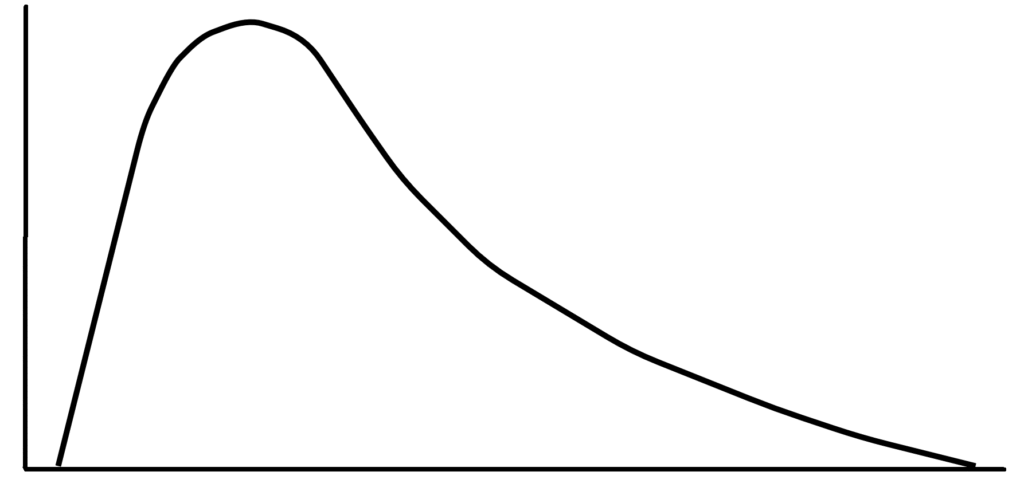
Eine Rechtsschiefe Verteilung sieht so aus. Man nennt sie rechtsschief, da die Kurve immer weiter abnimmt, je weiter man nach rechts geht. Wie ihr sehen könnt, haben wir links mehr Werte als rechts, deswegen nennt man sie auch Linkssteil. Zudem wissen wir, dass der Schiefekoeffizient größer als Null ist. Das heißt eine rechtsschiefe Verteilung nennt man auch positive Schiefe.
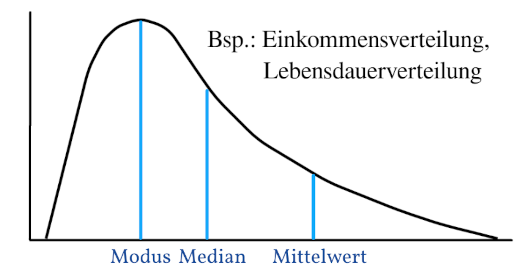
Beispiele für eine rechtsschiefe Verteilung wären die Einkommens- oder Lebensdauerverteilung. Das liegt einfach daran, dass es viele Leute gibt, die ähnlich viel verdienen und dann werden es immer weniger, die deutlich mehr verdienen.
Wie ihr vom Beitrag zu den Lagemaßen bereits wisst, erkennt man den Modus am Gipfel der Verteilung. Zudem wisst ihr, dass das arithmetische Mittel nicht robust gegenüber Ausreißern ist. Dadurch, dass einige Personen deutlich mehr verdienen als Andere, erhöht sich der Mittelwert. Und er verschiebt sich somit nach rechts. Der Median ist robuster gegenüber Ausreißern, das heißt er lässt sich nicht von diesen beeinflussen.
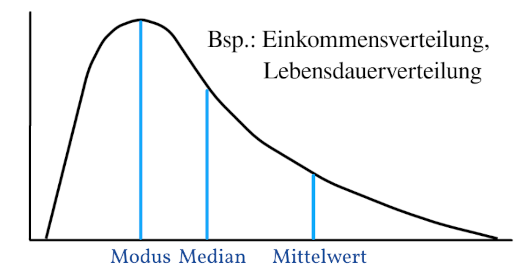
Somit sieht man an der Graphik schön, dass bei einer rechtsschiefen Verteilung generell der Modus kleiner ist als der Median und dieser kleiner als der Mittelwert ist.
$$ Modus < Median < Mittelwert $$
Linksschief
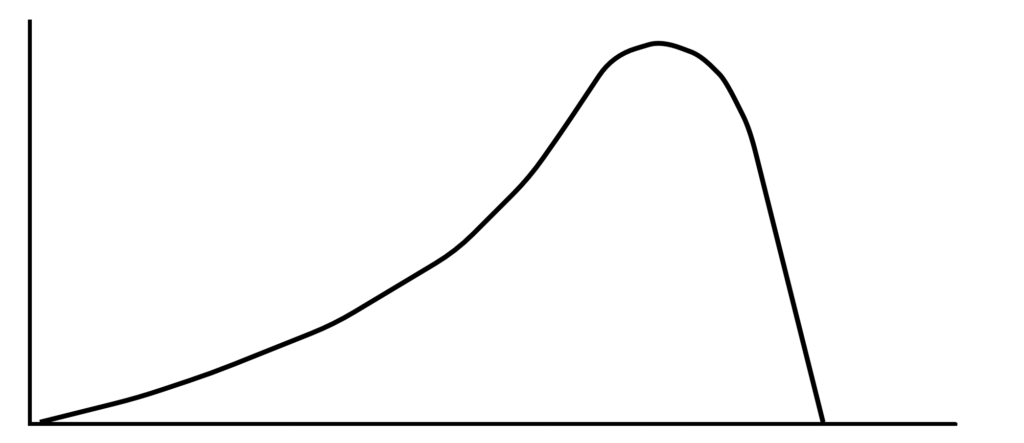
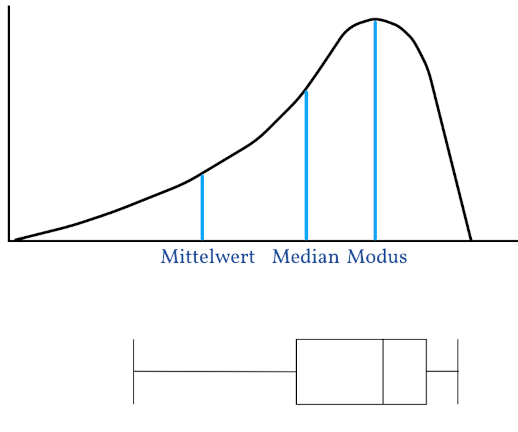
Die linksschiefe Verteilung ist das Gegenteil der rechtsschiefen Verteilung. Es befinden sich weniger Werte auf der linken Seite, deswegen Linksschief bzw. weil sich rechts mehr Werte befinden, nennt man es auch Rechtssteil. Der Schiefekoeffizient ist kleiner als Null, weswegen sie auch als negative Schiefe bezeichnet wird.
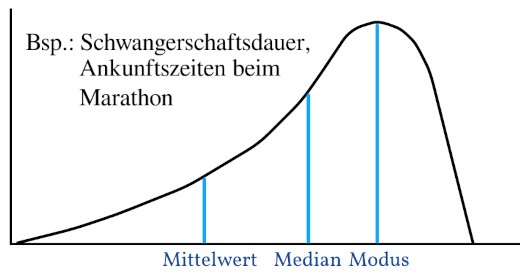
Beispiele für linksschiefe Verteilungen sind Schwangerschaftsdauer oder Ankunftszeiten bei einem Lauf, wie zum Beispiel dem Marathon. Die Mehrheit bei einem Lauf kommt zu ähnlichen Zeiten ins Ziel. Es gibt aber einige wenige, die deutlich schneller sind.
Der Modus befindet sich wieder beim Gipfel, die schnelleren Läufer verringern den Mittelwert, weswegen dieser deutlich weiter links liegt und der Median verschiebt sich auch etwas nach links. Somit ist bei einer linksschiefen Verteilung der Mittelwert kleiner als der Median und dieser ist kleiner als der Modus.
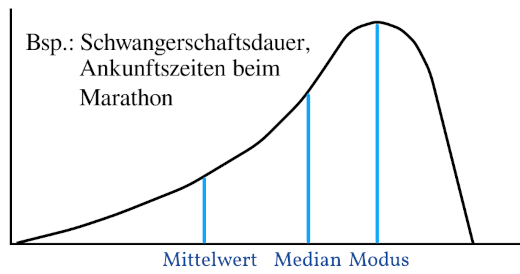
$$ Mittelwert < Median < Modus $$
Schiefe und Boxplots
Ob eine Verteilung rechts- oder linksschief ist, lässt sich auch anhand von Boxplots einfach erkennen.
Rechtsschief
Linksschief
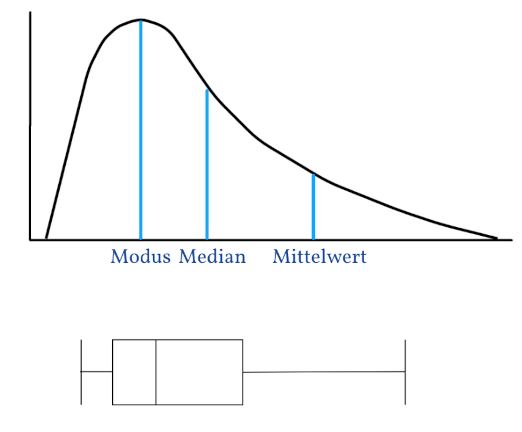
Ist die Box eher auf der linken Seite handelt es sich um eine rechtsschiefe Verteilung.
Liegt die Box eher auf der rechten Seite ist die Verteilung linksschief.
Bitte beachtet, dass dies im Allgemeinen so gehandhabt werden kann aber es gibt auch Ausnahmen.
Fechner’sche Lageregel
Das soeben Besprochene ist auch die Idee hinter der Fechner’schen Lageregel. Und zwar muss man im einfachsten Fall nur Modus, Median, bzw. Mittelwert miteinander vergleichen und schon kann man die Schiefe bestimmen. Wenn der Modus bzw. Median kleiner als der Mittelwert ist, dann ist es rechtsschief und andersherum ist es linksschief. Und sind die drei Lagemaße annähernd gleich groß, dann handelt es sich um eine symmetrische Verteilung.
Rechtsschief
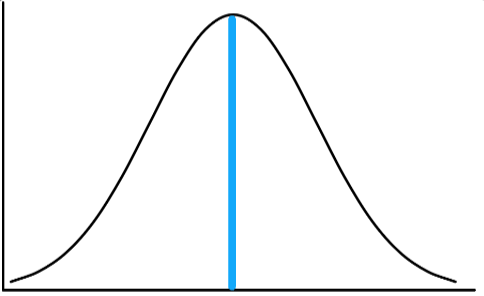
Symmetrisch
Linksschief
Schiefe – Erklärung
Heute geht es um die Schiefe.
- Wichtige Infos
- Schiefe anhand von Häufigkeitsverteilung
- Schiefe anhand von Boxplot
- Fechner’sche Lageregel
- Berechnungen (Quartils- und Momentschiefe)
Wichtiges Vorwissen zu diesem Beitrag sind die Lagemaße.
Außerdem ist es hilfreich, wenn ihr auch schon wisst was Boxplots sind und wie man die Standardabweichung berechnet.
Infos
Die Schiefe beschreibt die Stärke der Asymmetrie einer Verteilung und wird auf Englisch Skewness genannt. Eine symmetrische Verteilung hat eine Schiefe von Null. Falls sie nicht symmetrisch ist, wird sie als schief bezeichnet, wobei generell zwischen rechts- und linksschief unterschieden wird. Die Schiefe ist im Allgemeinen nicht normiert, sie kann also beliebig große Werte annehmen.
Es gibt viele verschiedene Ansätze zur Bestimmung der Schiefe, in diesem Video sehen wir uns die Fechner‘sche Lageregel, die Quartilsschiefe, die Person-Schiefemaße und die Momentschiefe an. Dabei gibt es zu allen Varianten eine kurze Erklärung und wie man diese berechnet.
Rechtsschief

Eine Rechtsschiefe Verteilung sieht so aus. Man nennt sie rechtsschief, da die Kurve immer weiter abnimmt, je weiter man nach rechts geht. Wie ihr sehen könnt, haben wir links mehr Werte als rechts, deswegen nennt man sie auch Linkssteil. Zudem wissen wir, dass der Schiefekoeffizient größer als Null ist. Das heißt eine rechtsschiefe Verteilung nennt man auch positive Schiefe.
Beispiele für eine rechtsschiefe Verteilung wären die Einkommens- oder Lebensdauerverteilung. Das liegt einfach daran, dass es viele Leute gibt, die ähnlich viel verdienen und dann werden es immer weniger, die deutlich mehr verdienen.
Wie ihr vom Beitrag zu den Lagemaßen bereits wisst, erkennt man den Modus am Gipfel der Verteilung. Zudem wisst ihr, dass das arithmetische Mittel nicht robust gegenüber Ausreißern ist. Dadurch, dass einige Personen deutlich mehr verdienen als Andere, erhöht sich der Mittelwert. Und er verschiebt sich somit nach rechts. Der Median ist robuster gegenüber Ausreißern, das heißt er lässt sich nicht von diesen beeinflussen.

Somit sieht man an der Graphik schön, dass bei einer rechtsschiefen Verteilung generell der Modus kleiner ist als der Median und dieser kleiner als der Mittelwert ist.
$$ Modus < Median < Mittelwert $$
Linksschief

Die linksschiefe Verteilung ist das Gegenteil der rechtsschiefen Verteilung. Es befinden sich weniger Werte auf der linken Seite, deswegen Linksschief bzw. weil sich rechts mehr Werte befinden, nennt man es auch Rechtssteil. Der Schiefekoeffizient ist kleiner als Null, weswegen sie auch als negative Schiefe bezeichnet wird.
Beispiele für linksschiefe Verteilungen sind Schwangerschaftsdauer oder Ankunftszeiten bei einem Lauf, wie zum Beispiel dem Marathon. Die Mehrheit bei einem Lauf kommt zu ähnlichen Zeiten ins Ziel. Es gibt aber einige wenige, die deutlich schneller sind.
Der Modus befindet sich wieder beim Gipfel, die schnelleren Läufer verringern den Mittelwert, weswegen dieser deutlich weiter links liegt und der Median verschiebt sich auch etwas nach links. Somit ist bei einer linksschiefen Verteilung der Mittelwert kleiner als der Median und dieser ist kleiner als der Modus.

$$ Mittelwert < Median < Modus $$
Schiefe und Boxplots
Ob eine Verteilung rechts- oder linksschief ist, lässt sich auch anhand von Boxplots einfach erkennen.
Rechtsschief
Linksschief


Ist die Box eher auf der linken Seite handelt es sich um eine rechtsschiefe Verteilung.
Liegt die Box eher auf der rechten Seite ist die Verteilung linksschief.
Bitte beachtet, dass dies im Allgemeinen so gehandhabt werden kann aber es gibt auch Ausnahmen.
Fechner’sche Lageregel
Das soeben Besprochene ist auch die Idee hinter der Fechner’schen Lageregel. Und zwar muss man im einfachsten Fall nur Modus, Median, bzw. Mittelwert miteinander vergleichen und schon kann man die Schiefe bestimmen. Wenn der Modus bzw. Median kleiner als der Mittelwert ist, dann ist es rechtsschief und andersherum ist es linksschief. Und sind die drei Lagemaße annähernd gleich groß, dann handelt es sich um eine symmetrische Verteilung.
Rechtsschief
Symmetrisch
Linksschief



