Spannweite
Hier geht’s um ein weiteres, sehr einfaches Streuungsmaß: Die Spannweite
- Was ist die Spannweite?
- Berechnung anhand eines einfachen Beispiels
Was ist die Spannweite?
Die Spannweite wird auf Englisch Range genannt und beschreibt die Differenz zwischen dem größten (Maximum) und dem kleinsten Wert (Minimum) der Stichprobe.
$$ R = x_{max} \: – \: x_{min} $$
Da die Spannweite aus diesen beiden Extremwerten berechnet wird, ist sie nicht robust gegenübern Ausreißern.
Beispiel Berechnung
Wir verwenden ein Beispiel, mit dem wir hier bei der Statistikquelle schon gut vertraut sind. Unsere bekannten (geordneten) Alterswerte von 10 Personen:
$$ 20, 21, 22, 22, 22, 24, 25, 25, 26, 28 $$
Für die Berechnung der Spannweite brauchen wir also nur das Maximum und das Minimum der Stichprobe.
$$\begin{aligned}x_{min} &= 20\\ x_{max} &= 28\end{aligned}$$
$$\begin{aligned}R &= x_{max} \: – \: x_{min}\\ R &= 28 – 20\\ R &= 8\end{aligned}$$
Als Spannweite erhalten wir den Wert 8 Jahre.
Interpretation: Alle Werte liegen in einem Bereich von 8 Jahren.
Auf dem folgenden Bild wird die Spannweite noch visuell (auch im Vergleich zum robusten Interquartilsabstand) dargestellt.
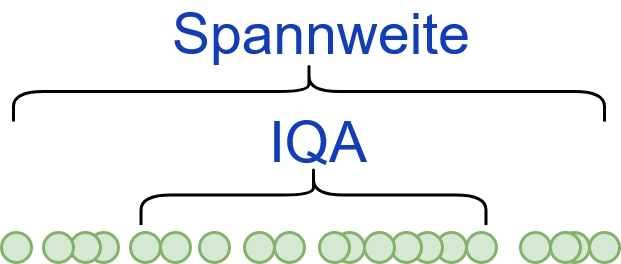
Spannweite
Hier geht’s um ein weiteres, sehr einfaches Streuungsmaß: Die Spannweite
- Was ist die Spannweite?
- Berechnung anhand eines einfachen Beispiels
Was ist die Spannweite?
Die Spannweite wird auf Englisch Range genannt und beschreibt die Differenz zwischen dem größten (Maximum) und dem kleinsten Wert (Minimum) der Stichprobe.
$$ R = x_{max} \: – \: x_{min} $$
Da die Spannweite aus diesen beiden Extremwerten berechnet wird, ist sie nicht robust gegenübern Ausreißern.
Beispiel Berechnung
Wir verwenden ein Beispiel, mit dem wir hier bei der Statistikquelle schon gut vertraut sind. Unsere bekannten (geordneten) Alterswerte von 10 Personen:
$$ 20, 21, 22, 22, 22, 24, 25, 25, 26, 28 $$
Für die Berechnung der Spannweite brauchen wir also nur das Maximum und das Minimum der Stichprobe.
$$\begin{aligned}x_{min} &= 20\\ x_{max} &= 28\end{aligned}$$
$$\begin{aligned}R &= x_{max} \: – \: x_{min}\\ R &= 28 – 20\\ R &= 8\end{aligned}$$
Als Spannweite erhalten wir den Wert 8 Jahre.
Interpretation: Alle Werte liegen in einem Bereich von 8 Jahren.
Auf dem folgenden Bild wird die Spannweite noch visuell (auch im Vergleich zum robusten Interquartilsabstand) dargestellt.