Tauche ein in unsere modebewusste Statistik-Welt.
Venn-Diagramme
- Erklärung
- Eigenschaften und Verwendung
- Darstellung von Ereignissen mittels Venn-Diagramm
- Berechnung von Wahrscheinlichkeiten mit Unterstützung von Venn-Diagrammen
- Intuition zu einigen Formeln
Es ist hilfreich, wenn ihr euch bereits den Einleitungsbeitrag zu Wahrscheinlichkeiten mit den Axiomen von Kolmogorow angesehen habt.
Erklärung
Venn-Diagramme sind nach dem britischen Mathematiker und Logiker John Venn benannt. Sie werden in der Wahrscheinlichkeitsrechnung und Mengenlehre dazu verwendet, Zusammenhänge zwischen 2 oder mehreren Ereignissen grafisch darzustellen. Ein Venn-Diagramm besteht aus einem Rechteck mit mehreren Kreisen.
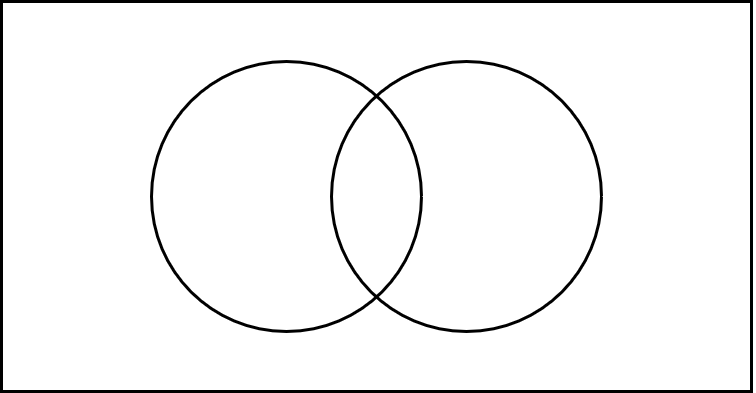
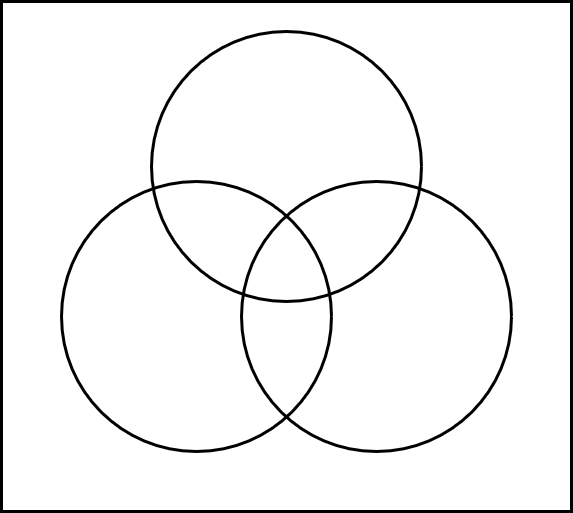
Das Rechteck stellt hier \(\Omega\) (sprich: Omega) dar. \(\Omega\) ist unser Ereignisraum. Die einzelnen Kreise präsentieren die jeweiligen Ereignisse. Die Größe der Kreise spielt keine Rolle und gibt uns dabei keine Auskunft über die Wahrscheinlichkeit des entsprechenden Ereignisses.
Venn-Diagramm für 2 Ereignisse
Hat man 2 Ereignisse A und B gegeben, kann man diese beiden Ereignisse und alle möglichen Operationen der beiden durch Venn-Diagramme veranschaulichen. Sehen wir uns einige Beispiele an.
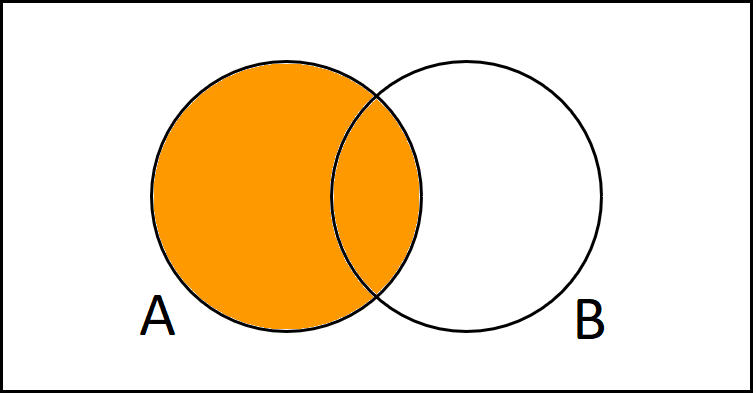
Reden wir einfach nur das über das Ereignis A, malen wir den Kreis von A gänzlich aus.
$$A$$
Das Komplement von A ist ja „das Gegenteil“, somit malen wir in diesem Fall alles außer A an.
$$A^c \text{ oder } \overline{A}$$
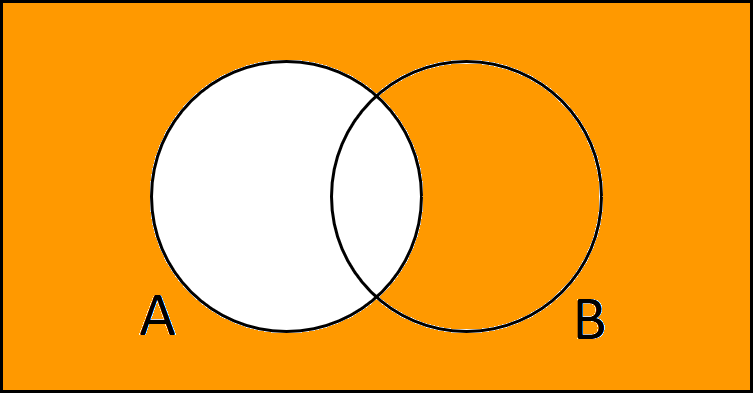
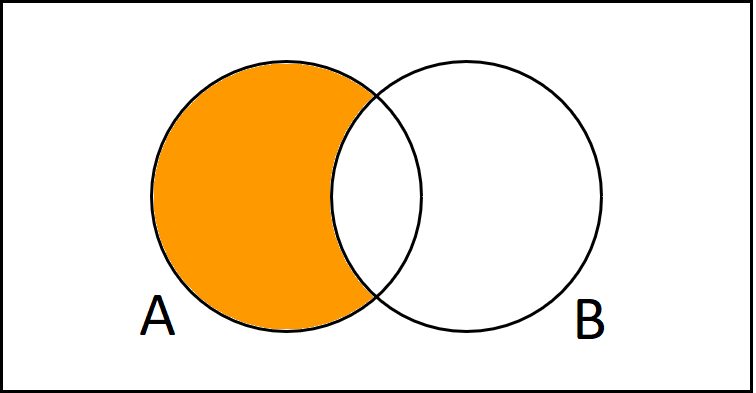
Wir können auch die Differenz, also A ohne B darstellen. Das wäre dann der Bereich von A, der sich nicht mit B überschneidet.
$$A\backslash B$$
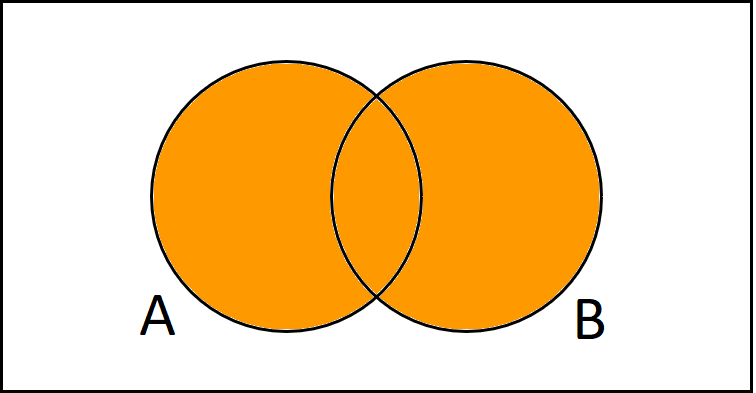
Die Vereinigung von A und B stellt man dar, indem man beide Kreise anmalt.
$$A \cup B$$
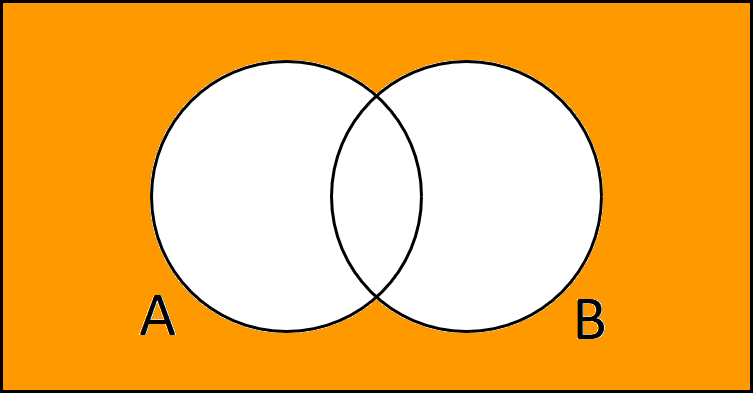
Für A vereinigt B Komplement lassen wir den Bereich von A vereinigt B weiß und malen den Rest an.
$${( A \cup B)}^c \text{ oder } \overline{A \cup B}$$
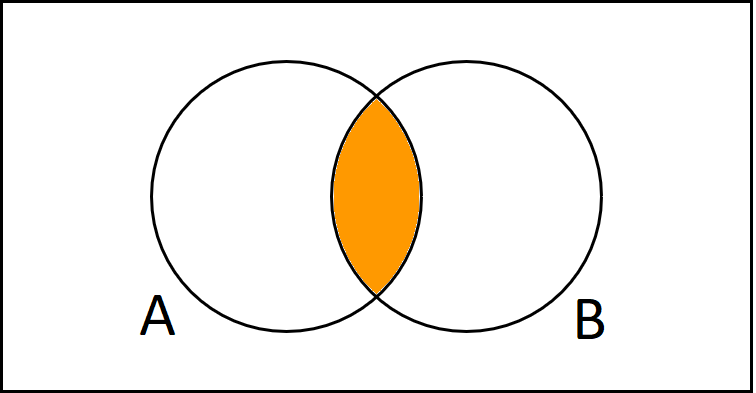
Die Schnittmenge von A und B ist der Bereich, wo sich die beiden Kreise überschneiden.
$$A \cap B$$
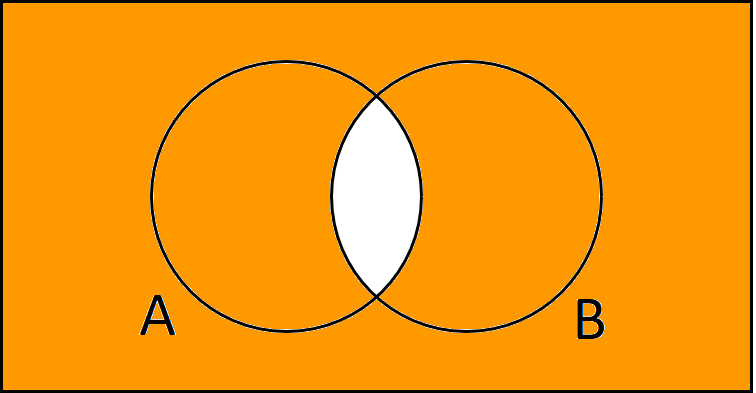
A geschnitten B Komplement ist natürlich dann alles andere außer der Schnittmenge.
$${( A \cap B )}^c \text{ oder } \overline{A \cap B}$$
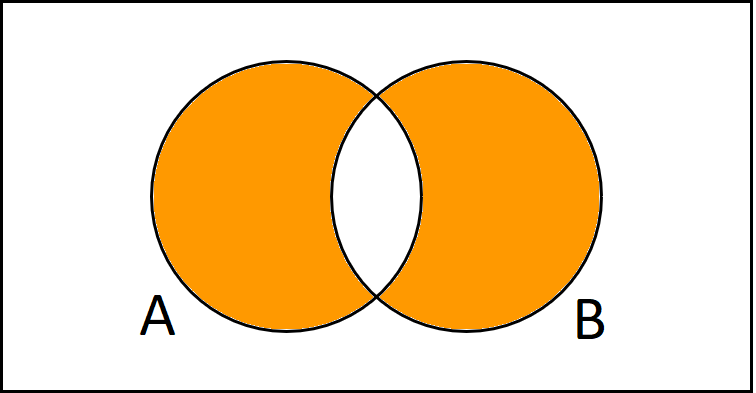
Die symmetrische Differenz lässt sich auf mehrere Arten beschreiben. Wir notieren sie hier mit A geschnitten B Komplement vereinigt mit A Komplement geschnitten B. Wir werden dann im Beispiel gleich noch sehen, wie man sich das auch selbst herleiten kann.
$$(A \cap B ^c) \cup A^c \cap B$$
$$\text{oder}$$
$$A \cap \overline{B} \cup \overline{A} \cap B$$
Beispiel
Anna und Basti lernen unabhängig voneinander für eine schwere Statistikprüfung. Anna hat sich zur Vorbereitung Videos und Beiträge der Statistikquelle angesehen. Basti hat einfach so gelernt. Wir ordnen Anna eine Wahrscheinlichkeit von 90% zu, die Prüfung zu bestehen. Bei Basti sagen wir, es sind 40%.
Wir wollen nun die Wahrscheinlichkeiten berechnen, dass
- beide die Prüfung schaffen
- mindestens 1 der beiden die Prüfung schafft
- niemand die Prüfung schafft
- nur Anna die Prüfung schafft
- höchstens 1 die Prüfung schafft
- genau einer die Prüfung schafft
Bevor wir starten, eben wir den gegebenen Informationen Namen d.h. wir bestimmen kurz unsere Variablen. A steht dafür, dass Anna und B dafür, dass Basti die Prüfung schafft. Wir kennen bereits auch die beiden Wahrscheinlichkeiten. Somit haben wir P von A gleich 0,9 und P von B gleich 0,4.
$$A = \text{Anna schafft die Prüfung} \quad P(A) = 0.9$$
$$B= \text{Basti schafft die Prüfung} \quad P(B) = 0.4$$
- P(beide bestehen)
Wenn wir das als Venn-Diagramm zeichnen wollen, müssen wir somit die Schnittmenge anmalen, weil nur in diesem Bereich beide die Prüfung bestanden haben. Die beiden Ereignisse sind unabhängig, weswegen wir die Wahrscheinlichkeiten multiplizieren, um die Schnittmenge zu erhalten.
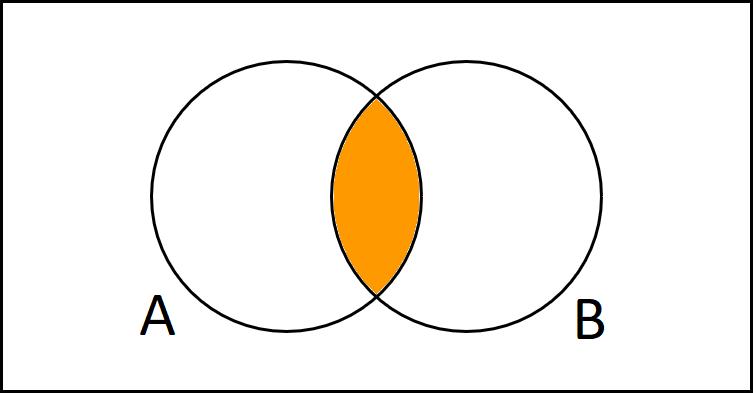
$$P(A \cap B) = P(A) \cdot P(B) = 0.9 \cdot 0.4 = 0.36$$
Die Wahrscheinlichkeit, dass beide die Prüfung bestehen ist somit 36%.
2. P(mind. 1 besteht)
Mindestens 1 besteht, bedeutet ja, dass nur Anna die Prüfung besteht oder nur Basti oder beide. Man merkt, dass man dieses Ereignis durch die Vereinigung von A und B beschreiben kann.
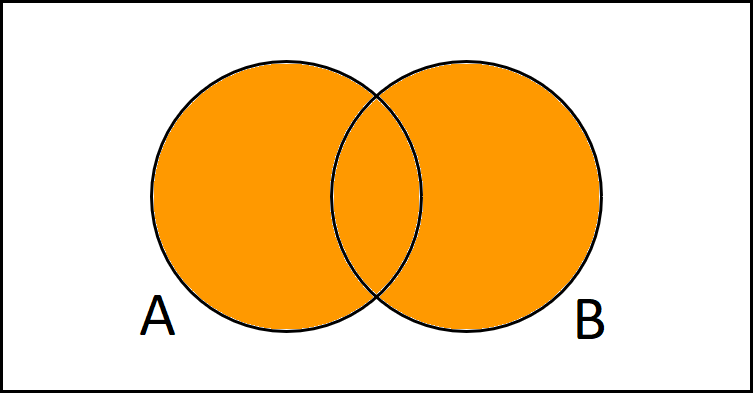
Wenn wir die angemalte Fläche bestimmen wollen, können wir ja einfach die beiden Kreise von A und B miteinander addieren.
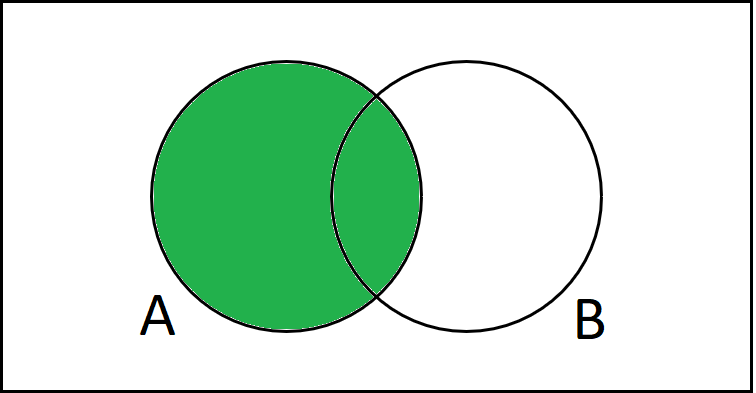
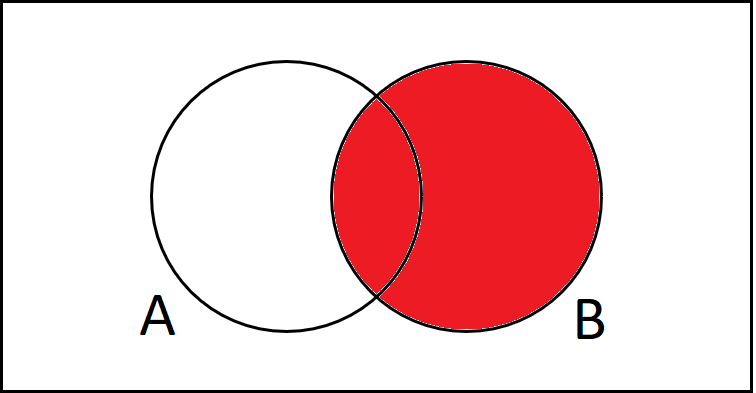
Wenn wir aber den Kreis von A plus den Kreis von B rechnen, sehen wir, dass wir die Schnittmenge doppelt genommen haben.
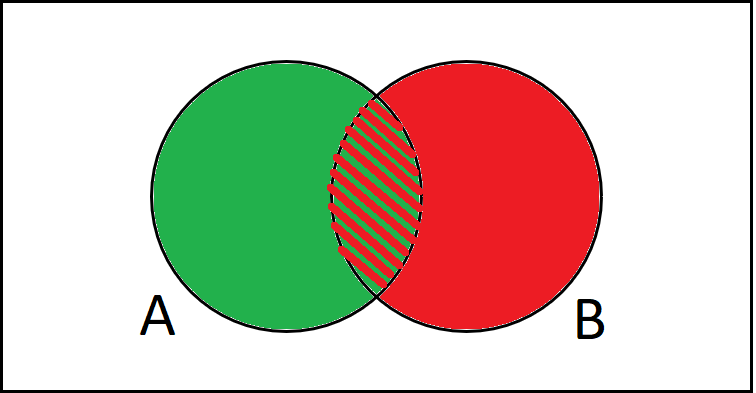
Deswegen müssen wir sie noch einmal abziehen. Und so habt ihr euch die Formel für die Vereinigung einfach selbst hergeleitet
$$P(A \cup B) = P(A) + P(B) – P(A \cap B) = 0.9 + 0.4 – 0.36 = 0.94$$
Wir haben also eine Wahrscheinlichkeit von 94%, dass mindestens einer die Prüfung schafft.
3. P(niemand besteht)
Hier betrachten wir das Ereignis, dass weder Anna noch Basti die Prüfung schaffen. Somit müssen wir alles außerhalb der Kreise anmalen. Alles, was dann weiß geblieben ist, ist ja die Vereinigung. Wir wollen jetzt das Gegenteil berechnen. Das ist A vereinigt B Komplement. Ein Komplementärereignis können wir ganz einfach berechnen, indem wir 1 der Wahrscheinlichkeit des Ereignisses rechnen.
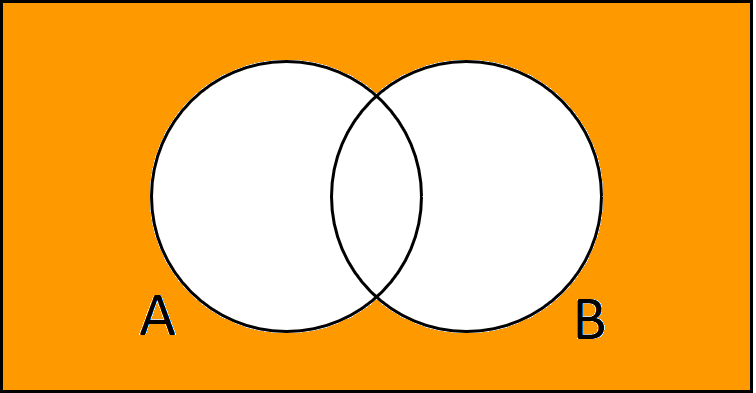
$$ \begin{align} P(\overline{A \cup B}) &= 1 – P(A \cup B) \\ &= 1 – 0.94 \\ &= 0.06 \end{align}$$
MIt 6-prozentiger Wahrscheinlichkeit besteht niemand die Prüfung.
4. P(nur Anna besteht)
In diesem Fall malen nun den Kreis von A an, jedoch ohne die Schnittmenge, da Basti ja nicht besteht. So gehen wir auch rechnerisch vor. Wir ziehen die Wahrscheinlichkeit der Schnittmenge von der Wahrscheinlichkeit für der Ereignis A ab.

$$\begin{align} P(A\backslash B) &= P(A) – P(A \cap B) \\ &= 0.9 – 0.36 \\ &= 0.54 \end{align}$$
Mit 54-prozentiger Wahrscheinlichkeit besteht nur Anna.
5. P(höchstens 1 besteht)
Dieses Ereignis setzt sich aus 3 Ereignissen zusammen. Entweder niemand besteht, nur Anna oder nur Basti. Im Venn-Diagramm malt man alles an, außer der Schnittmenge. Somit können wir die Wahrscheinlichkeit ganz einfach wieder berechnen, in dem wir das Gegenteil (= Komplement) der Schnittmenge nehmen.
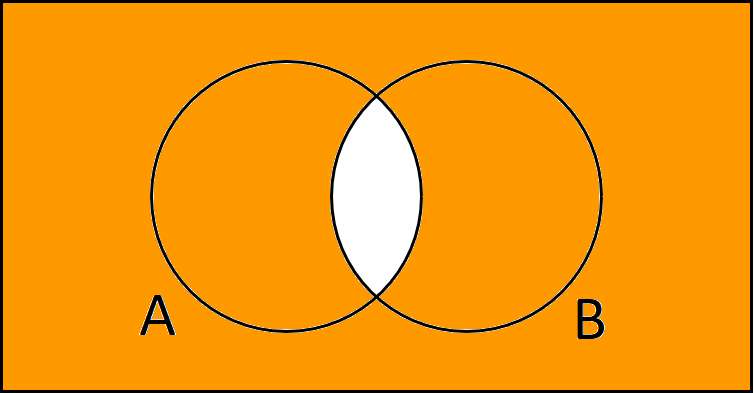
$$\begin{align} P(\overline{A \cap B}) &= 1- P(A \cap B)\\ &= 1 – 0.36\\ &= 0.64 \end{align}$$
Die Wahrscheinlichkeit, dass höchstens einer die Prüfung besteht, ist also 64%.
5. P(genau 1 besteht)
Hier lassen wir die Fläche um die Kreise herum frei, weil dieser Bereich ja dafür steht, dass niemand die Prüfung schafft. Es kann jetzt sein, dass Anna alleine die Prüfung schafft oder, dass Basti die Prüfung schafft. Wir malen also beide Kreise an, jedoch ohne die Schnittmenge.

Das ist, wie oben schon erwähnt, die symmetrische Differenz. Leiten wir uns her, wie man sie berechnet:
Das Venn-Diagramm, so wie wir es angemalt haben bedeutet ja nichts anderes als, dass Anna die Prüfung schafft und Basti nicht oder dass Anna die Prüfung nicht schafft und Basti, aber die Prüfung besteht.
Man bezeichnet die Vereinigung auch als „oder“ und die Schnittmenge auch als „und“. Somit können wir das oben geschriebene direkt in unsere Formel umwandeln. Formeln sind ja einfach eine Abkürzung für uns.
$$\cup \quad \text{„und“} \qquad \cap \quad \text{„oder“}$$
„Anna besteht“ schrieben wir als A, „und“ als Schnittmenge \(\cap\), „Basti nicht“ ist das Gegenteil davon, dass Basti die Prüfung besteht \(\overline{B}\).
\(A \cap \overline{B}\) beschreibt also den linken Kreis. „Oder“ steht für Vereinigung \(\cup \), „Anna nicht“ wäre dann \(\overline{A}\) „und“ \(\cap \), „Basti schon“ B.
$$A \cap \overline{B} \cup \overline{A} \cap B$$
Somit habt ihr diese doch etwas komplizierter aussehende Formel ganz einfach selbst hergeleitet.
$$\begin{align} P(A \cap \overline{B} \cup \overline{A} \cap B) &= P(A) \cdot P(\overline{B}) + P(\overline{A}) \cdot P(B) \\ &= 0.9\cdot 0.6 + 0.1 \cdot 0.4 \\& = 0.58\end{align}$$
Einfacher:
Wenn ihr so wie in unserem Fall zuvor schon Vereinigung und Schnittmenge berechnet habt, könnt ihr dasselbe auch berechnen, in dem ihr die Schnittmenge von der Vereinigung abzieht.
$$P((A \cup B) – (A \cap B)) = 0.94 – 0.36 = 0.58$$
Venn-Diagramme
- Erklärung
- Eigenschaften und Verwendung
- Darstellung von Ereignissen mittels Venn-Diagramm
- Berechnung von Wahrscheinlichkeiten mit Unterstützung von Venn-Diagrammen
- Intuition zu einigen Formeln
Es ist hilfreich, wenn ihr euch bereits den Einleitungsbeitrag zu Wahrscheinlichkeiten mit den Axiomen von Kolmogorow angesehen habt.
Erklärung
Venn-Diagramme sind nach dem britischen Mathematiker und Logiker John Venn benannt. Sie werden in der Wahrscheinlichkeitsrechnung und Mengenlehre dazu verwendet, Zusammenhänge zwischen 2 oder mehreren Ereignissen grafisch darzustellen. Ein Venn-Diagramm besteht aus einem Rechteck mit mehreren Kreisen.


Das Rechteck stellt hier \(\Omega\) (sprich: Omega) dar. \(\Omega\) ist unser Ereignisraum. Die einzelnen Kreise präsentieren die jeweiligen Ereignisse. Die Größe der Kreise spielt keine Rolle und gibt uns dabei keine Auskunft über die Wahrscheinlichkeit des entsprechenden Ereignisses.
Venn-Diagramm für 2 Ereignisse
Hat man 2 Ereignisse A und B gegeben, kann man diese beiden Ereignisse und alle möglichen Operationen der beiden durch Venn-Diagramme veranschaulichen. Sehen wir uns einige Beispiele an.

Reden wir einfach nur das über das Ereignis A, malen wir den Kreis von A gänzlich aus.
$$A$$
Das Komplement von A ist ja „das Gegenteil“, somit malen wir in diesem Fall alles außer A an.
$$A^c \text{ oder } \overline{A}$$


Wir können auch die Differenz, also A ohne B darstellen. Das wäre dann der Bereich von A, der sich nicht mit B überschneidet.
$$A\backslash B$$
Die Vereinigung von A und B stellt man dar, indem man beide Kreise anmalt.
$$A \cup B$$


Für A vereinigt B Komplement lassen wir den Bereich von A vereinigt B weiß und malen den Rest an.
$${( A \cup B)}^c \text{ oder } \overline{A \cup B}$$
Die Schnittmenge von A und B ist der Bereich, wo sich die beiden Kreise überschneiden.
$$A \cap B$$


A geschnitten B Komplement ist natürlich dann alles andere außer der Schnittmenge.
$${( A \cap B )}^c \text{ oder } \overline{A \cap B}$$
Die symmetrische Differenz lässt sich auf mehrere Arten beschreiben. Wir notieren sie hier mit A geschnitten B Komplement vereinigt mit A Komplement geschnitten B. Wir werden dann im Beispiel gleich noch sehen, wie man sich das auch selbst herleiten kann.
$$(A \cap B ^c) \cup A^c \cap B$$
$$\text{oder}$$
$$A \cap \overline{B} \cup \overline{A} \cap B$$

Beispiel
Anna und Basti lernen unabhängig voneinander für eine schwere Statistikprüfung. Anna hat sich zur Vorbereitung Videos und Beiträge der Statistikquelle angesehen. Basti hat einfach so gelernt. Wir ordnen Anna eine Wahrscheinlichkeit von 90% zu, die Prüfung zu bestehen. Bei Basti sagen wir, es sind 40%.
Wir wollen nun die Wahrscheinlichkeiten berechnen, dass
- beide die Prüfung schaffen
- mindestens 1 der beiden die Prüfung schafft
- niemand die Prüfung schafft
- nur Anna die Prüfung schafft
- höchstens 1 die Prüfung schafft
- genau einer die Prüfung schafft
Bevor wir starten, eben wir den gegebenen Informationen Namen d.h. wir bestimmen kurz unsere Variablen. A steht dafür, dass Anna und B dafür, dass Basti die Prüfung schafft. Wir kennen bereits auch die beiden Wahrscheinlichkeiten. Somit haben wir P von A gleich 0,9 und P von B gleich 0,4.
$$A = \text{Anna schafft die Prüfung} \quad P(A) = 0.9$$
$$B= \text{Basti schafft die Prüfung} \quad P(B) = 0.4$$
- P(beide bestehen)
Wenn wir das als Venn-Diagramm zeichnen wollen, müssen wir somit die Schnittmenge anmalen, weil nur in diesem Bereich beide die Prüfung bestanden haben. Die beiden Ereignisse sind unabhängig, weswegen wir die Wahrscheinlichkeiten multiplizieren, um die Schnittmenge zu erhalten.

$$P(A \cap B) = P(A) \cdot P(B) = 0.9 \cdot 0.4 = 0.36$$
Die Wahrscheinlichkeit, dass beide die Prüfung bestehen ist somit 36%.
2. P(mind. 1 besteht)
Mindestens 1 besteht, bedeutet ja, dass nur Anna die Prüfung besteht oder nur Basti oder beide. Man merkt, dass man dieses Ereignis durch die Vereinigung von A und B beschreiben kann.

Wenn wir die angemalte Fläche bestimmen wollen, können wir ja einfach die beiden Kreise von A und B miteinander addieren.


Wenn wir aber den Kreis von A plus den Kreis von B rechnen, sehen wir, dass wir die Schnittmenge doppelt genommen haben.

Deswegen müssen wir sie noch einmal abziehen. Und so habt ihr euch die Formel für die Vereinigung einfach selbst hergeleitet
$$P(A \cup B) = P(A) + P(B) – P(A \cap B) = 0.9 + 0.4 – 0.36 = 0.94$$
Wir haben also eine Wahrscheinlichkeit von 94%, dass mindestens einer die Prüfung schafft.
3. P(niemand besteht)
Hier betrachten wir das Ereignis, dass weder Anna noch Basti die Prüfung schaffen. Somit müssen wir alles außerhalb der Kreise anmalen. Alles, was dann weiß geblieben ist, ist ja die Vereinigung. Wir wollen jetzt das Gegenteil berechnen. Das ist A vereinigt B Komplement. Ein Komplementärereignis können wir ganz einfach berechnen, indem wir 1 der Wahrscheinlichkeit des Ereignisses rechnen.

$$ \begin{align} P(\overline{A \cup B}) &= 1 – P(A \cup B) \\ &= 1 – 0.94 \\ &= 0.06 \end{align}$$
MIt 6-prozentiger Wahrscheinlichkeit besteht niemand die Prüfung.
4. P(nur Anna besteht)
In diesem Fall malen nun den Kreis von A an, jedoch ohne die Schnittmenge, da Basti ja nicht besteht. So gehen wir auch rechnerisch vor. Wir ziehen die Wahrscheinlichkeit der Schnittmenge von der Wahrscheinlichkeit für der Ereignis A ab.

$$\begin{align} P(A\backslash B) &= P(A) – P(A \cap B) \\ &= 0.9 – 0.36 \\ &= 0.54 \end{align}$$
Mit 54-prozentiger Wahrscheinlichkeit besteht nur Anna.
5. P(höchstens 1 besteht)
Dieses Ereignis setzt sich aus 3 Ereignissen zusammen. Entweder niemand besteht, nur Anna oder nur Basti. Im Venn-Diagramm malt man alles an, außer der Schnittmenge. Somit können wir die Wahrscheinlichkeit ganz einfach wieder berechnen, in dem wir das Gegenteil (= Komplement) der Schnittmenge nehmen.

$$\begin{align} P(\overline{A \cap B}) &= 1- P(A \cap B)\\ &= 1 – 0.36\\ &= 0.64 \end{align}$$
Die Wahrscheinlichkeit, dass höchstens einer die Prüfung besteht, ist also 64%.
5. P(genau 1 besteht)
Hier lassen wir die Fläche um die Kreise herum frei, weil dieser Bereich ja dafür steht, dass niemand die Prüfung schafft. Es kann jetzt sein, dass Anna alleine die Prüfung schafft oder, dass Basti die Prüfung schafft. Wir malen also beide Kreise an, jedoch ohne die Schnittmenge.

Das ist, wie oben schon erwähnt, die symmetrische Differenz. Leiten wir uns her, wie man sie berechnet:
Das Venn-Diagramm, so wie wir es angemalt haben bedeutet ja nichts anderes als, dass Anna die Prüfung schafft und Basti nicht oder dass Anna die Prüfung nicht schafft und Basti, aber die Prüfung besteht.
Man bezeichnet die Vereinigung auch als „oder“ und die Schnittmenge auch als „und“. Somit können wir das oben geschriebene direkt in unsere Formel umwandeln. Formeln sind ja einfach eine Abkürzung für uns.
$$\cup \quad \text{„und“} \qquad \cap \quad \text{„oder“}$$
„Anna besteht“ schrieben wir als A, „und“ als Schnittmenge \(\cap\), „Basti nicht“ ist das Gegenteil davon, dass Basti die Prüfung besteht \(\overline{B}\).
\(A \cap \overline{B}\) beschreibt also den linken Kreis. „Oder“ steht für Vereinigung \(\cup \), „Anna nicht“ wäre dann \(\overline{A}\) „und“ \(\cap \), „Basti schon“ B.
$$A \cap \overline{B} \cup \overline{A} \cap B$$
Somit habt ihr diese doch etwas komplizierter aussehende Formel ganz einfach selbst hergeleitet.
$$\begin{align} P(A \cap \overline{B} \cup \overline{A} \cap B) &= P(A) \cdot P(\overline{B}) + P(\overline{A}) \cdot P(B) \\ &= 0.9\cdot 0.6 + 0.1 \cdot 0.4 \\& = 0.58\end{align}$$
Einfacher:
Wenn ihr so wie in unserem Fall zuvor schon Vereinigung und Schnittmenge berechnet habt, könnt ihr dasselbe auch berechnen, in dem ihr die Schnittmenge von der Vereinigung abzieht.
$$P((A \cup B) – (A \cap B)) = 0.94 – 0.36 = 0.58$$
