Tauche ein in unsere modebewusste Statistik-Welt.
Boxplot zeichnen
Hier lernt ihr ganz genau, wie man einen Boxplot zeichnet. Eine allgemeine Erklärung zum Boxplot findet ihr in diesem separaten Beitrag.
- Daten vorstellen
- Boxplot zeichnen
- Interpretation mit Grafiken
- Ausreißer einzeichnen
Daten
Als Beispieldaten verwenden wir das monatliche Nettoeinkommen von 20 Personen.
| 800 € | 1 200 € | 1 400 € | 2 000 € |
| 900 € | 1 250 € | 1 500 € | 2 500 € |
| 1 100 € | 1 300 € | 1 500 € | 2 600 € |
| 1 150 € | 1 300 € | 1 600 € | 2 700 € |
| 1 200 € | 1 400 € | 1 800 € | 2 800 € |
Die Werte, die wir fürs Zeichnen des Boxplots brauchen, sind folgende:
Das Minimum und Maximum betragen hier 800 bzw. 2800€. Der Median ist 1400€ und Q1 sowie Q3 betragen in diesem Beispiel 1200 bzw. 1900€.
$$x_{MIN} = 800€ \quad x_{MAX} = 2800€ \quad \bar{x}_M = 1400€$$
$$Q_1 = 1200€ \quad Q_3 = 1900€$$
Wie man diese Werte berechnen kann, seht ihr im Beitrag zu den Quantilen.
Das Zeichnen des Boxplots

Wir starten mit einem Zahlenstrahl, auf dem alle unsere Datenpunkte abgebildet werden können.

Als ersten Schritt zeichnen wir das Minimum ein. Das ist der kleine Anfangsstrich unseres Boxplots.
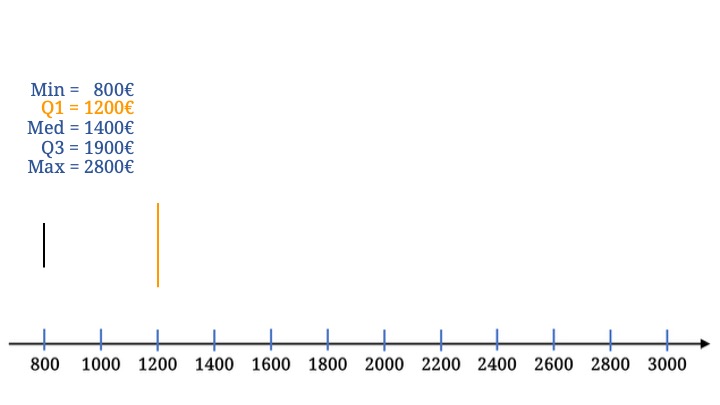
Dann zeichnen wir den Anfang der Box beim Wert des ersten Quartils.
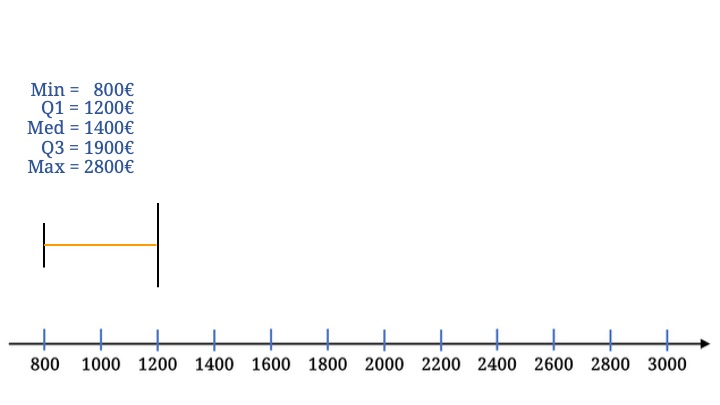
Die Verbindungslinie des Minimums und des ersten Quartils bildet den linken Whisker.

Beim dritten Quartil zeichnen wir das Ende der Box.
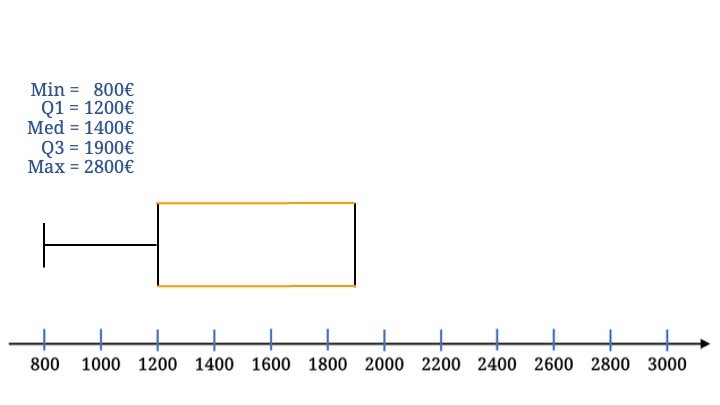
Hier vervollständigen wir den Rahmen der Box.

Abgeschlossen wird die Box durch das Einzeichnen des Medians.
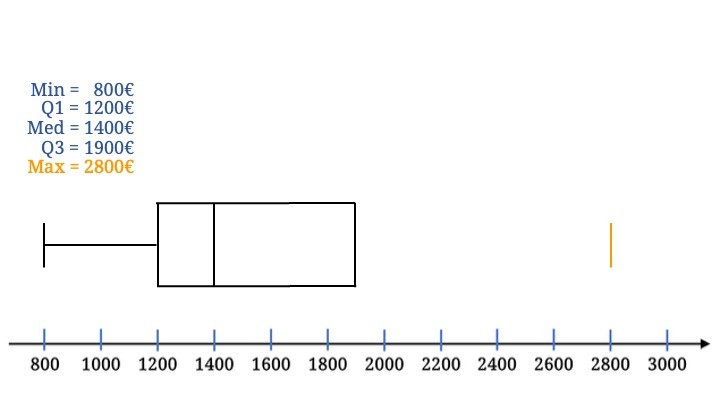
Das rechte Ende des Boxplots bildet das Maximum; der Strich ist gleich groß wie der des Minimums.
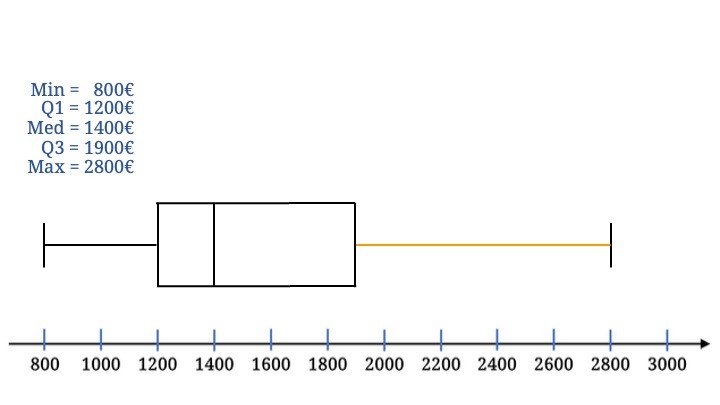
Der rechte Whisker vollendet den Boxplot.

Und fertig ist unser Boxplot!
Ihr seht schon, der Boxplot zeigt uns unsere Daten jetzt viel übersichtlicher, allerdings müssen wir auch einen Informationsverlust in Kauf nehmen. Der Boxplot zeigt uns nur eine Zusammenfassung der Daten. Wir wissen hier nicht mehr exakt, wie viel einzelne Personen verdienen. Außerdem wäre es uns nicht möglich, anhand des Boxplots zum Beispiel Mittelwert oder Standardabweichung zu berechnen.
Da wir den Boxplot jetzt gezeichnet haben, können wir einfach den Interquartilsabstand (IQA) und die Spannweite (R) ablesen.
$$IQA = Q_3 – Q_1 \quad R = x_{MAX} – x_{MIN}$$
Die Differenz von unterem (Q1) zum oberen Endes (Q3) der Box beträgt 700 und von Minimum zu Maximum 2000€. Das heißt:
$$IQA = 1900€ – 1200€ = 700€ \quad R = 2800€ – 800€ = 2000€$$
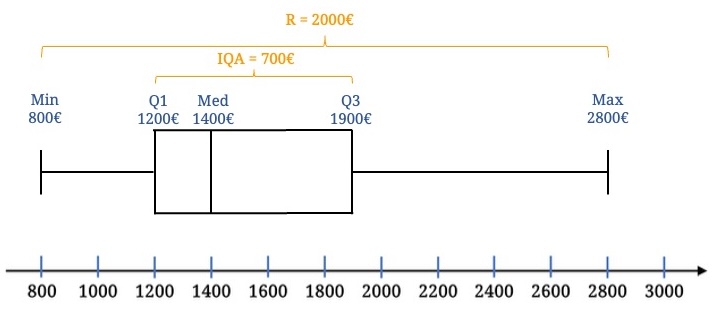
Interpretation
Anhand des Boxplots können wir nun viele Aussagen über die Stichprobe treffen. Q1 beträgt 1200€, somit verdienen 25% der Stichprobe weniger als 1200€ und 75% mehr als 1200€.


Q3 ist 1900€, also verdienen 75% weniger als 1900€ und 25% mehr als 1900€.

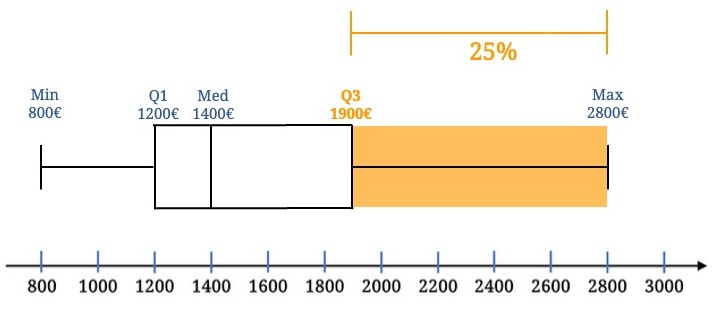
Der Median beträgt 1400€, also verdient eine Hälfte weniger, die andere Hälfte mehr als 1400€.
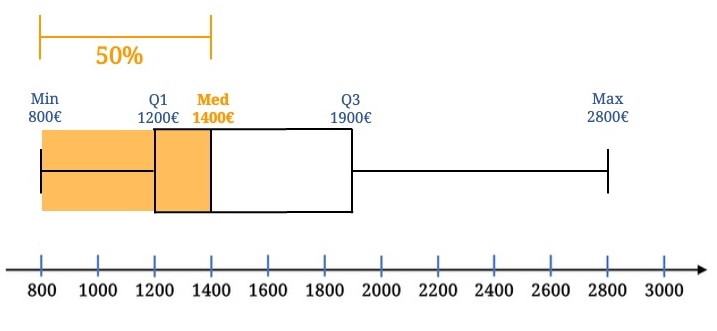
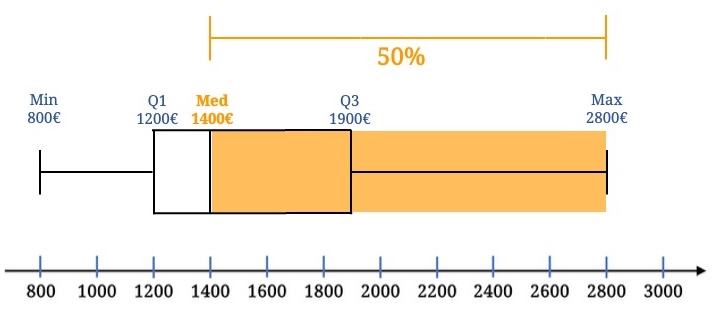
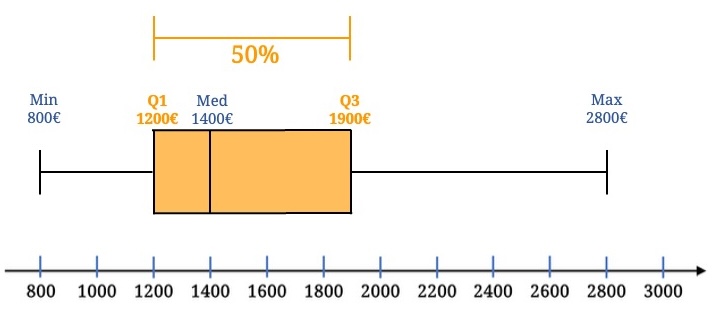
Und die Interquartilsdistanz ist 700€, also liegen die mittleren 50% innerhalb des Intervalls 1200€ bis 1900€.
Das Zeichnen von Ausreißern
Zum Zeichnen von Ausreißern nehmen wir an, die letzte Person unseres Beispiels würde nun 3200€ verdienen. Bis auf das Maximum bleiben die restlichen Lagemaße gleich wie zuvor.
$$x_{MIN} = 800€ \quad x_{MAX} = 3200€ \quad \bar{x}_M = 1400$$
$$Q_1 = 1200 \quad Q_3 = 1900$$
Ein Punkt gilt aus Ausreißer, wenn er mehr als das 1.5-fache des Interquartilsabstand von der Box dh. entweder von \(Q_1\) oder \(Q_3\) entfernt ist.
$$IQA = 1900€ – 1200€ = 700€ \text{ (wie vorher schon berechnet)}$$
Das 1.5-fache des Interquartilsabstand ist damit 1050€.
$$1.5 * IQA = 1.5 * 700 = 1050$$
Die untere Grenze (UG) und obere Grenze (OG) des Intervalls, in dem Werte keine Ausreißer sind, ergibt sich wie folgt:
$$\begin{align}UG &= Q_1 – 1.5*IQA \\ UG &= 1200 – 1050 \\ UG &= 150\end{align}$$
$$\begin{align}OG &= Q_3 + 1.5*IQA \\ OG &= 1900 + 1050 \\ UG &= 2950\end{align}$$
Das Intervall ist also
$$[150€; 2950€]$$
und der Wert 3200€ liegt außerhalb des Intervalls und ist damit ein Ausreißer.
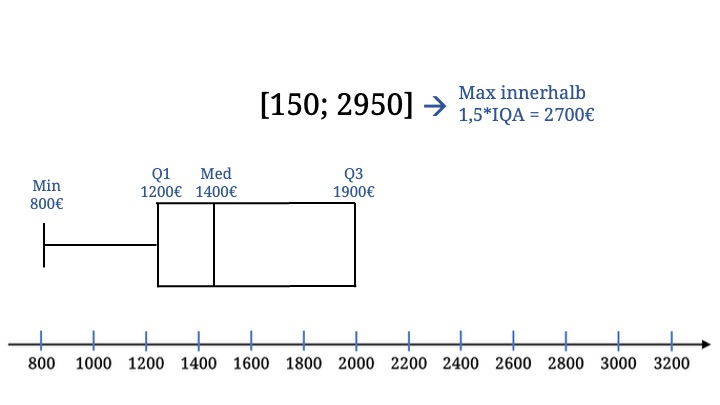
Wir starten mit einem unvollständigen Boxplot.

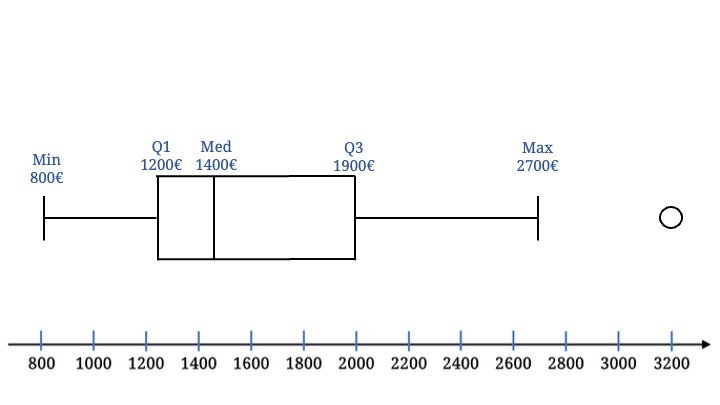
Als korrektes Maximum müssen wir hier den höchsten Wert nehmen, der noch im gerade ausgerechneten Intervall liegt.

Damit ist der Boxplot bis auf den Ausreißer komplett.
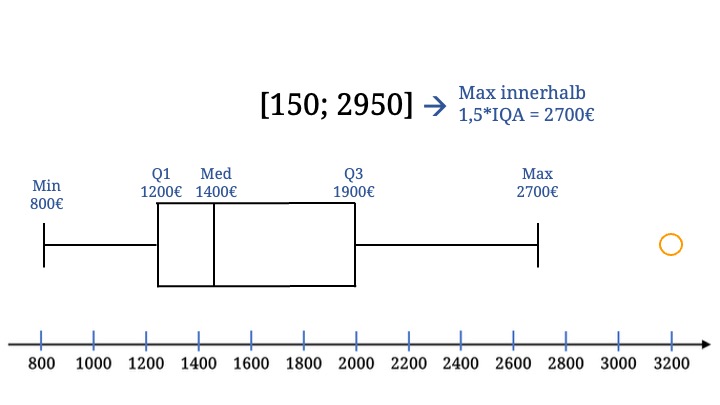
Der Ausreißer wird einfach als Ring auf der gleichen Höhe gezeichnet wie der Rest des Boxplots.
Also so schwer war das ja gar nicht!
Boxplot zeichnen
Hier lernt ihr ganz genau, wie man einen Boxplot zeichnet. Eine allgemeine Erklärung zum Boxplot findet ihr in diesem separaten Beitrag.
- Daten vorstellen
- Boxplot zeichnen
- Interpretation mit Grafiken
- Ausreißer einzeichnen
Daten
Als Beispieldaten verwenden wir das monatliche Nettoeinkommen von 20 Personen.
| 800 € | 1 200 € | 1 400 € | 2 000 € |
| 900 € | 1 250 € | 1 500 € | 2 500 € |
| 1 100 € | 1 300 € | 1 500 € | 2 600 € |
| 1 150 € | 1 300 € | 1 600 € | 2 700 € |
| 1 200 € | 1 400 € | 1 800 € | 2 800 € |
Die Werte, die wir fürs Zeichnen des Boxplots brauchen, sind folgende:
Das Minimum und Maximum betragen hier 800 bzw. 2800€. Der Median ist 1400€ und Q1 sowie Q3 betragen in diesem Beispiel 1200 bzw. 1900€.
$$x_{MIN} = 800€ \quad x_{MAX} = 2800€ \quad \bar{x}_M = 1400€$$
$$Q_1 = 1200€ \quad Q_3 = 1900€$$
Wie man diese Werte berechnen kann, seht ihr im Beitrag zu den Quantilen.
Das Zeichnen des Boxplots

Wir starten mit einem Zahlenstrahl, auf dem alle unsere Datenpunkte abgebildet werden können.

Als ersten Schritt zeichnen wir das Minimum ein. Das ist der kleine Anfangsstrich unseres Boxplots.

Dann zeichnen wir den Anfang der Box beim Wert des ersten Quartils.

Die Verbindungslinie des Minimums und des ersten Quartils bildet den linken Whisker.

Beim dritten Quartil zeichnen wir das Ende der Box.

Hier vervollständigen wir den Rahmen der Box.

Abgeschlossen wird die Box durch das Einzeichnen des Medians.

Das rechte Ende des Boxplots bildet das Maximum; der Strich ist gleich groß wie der des Minimums.

Der rechte Whisker vollendet den Boxplot.

Und fertig ist unser Boxplot!
Ihr seht schon, der Boxplot zeigt uns unsere Daten jetzt viel übersichtlicher, allerdings müssen wir auch einen Informationsverlust in Kauf nehmen. Der Boxplot zeigt uns nur eine Zusammenfassung der Daten. Wir wissen hier nicht mehr exakt, wie viel einzelne Personen verdienen. Außerdem wäre es uns nicht möglich, anhand des Boxplots zum Beispiel Mittelwert oder Standardabweichung zu berechnen.
Da wir den Boxplot jetzt gezeichnet haben, können wir einfach den Interquartilsabstand (IQA) und die Spannweite (R) ablesen.
$$IQA = Q_3 – Q_1 \quad R = x_{MAX} – x_{MIN}$$
Die Differenz von unterem (Q1) zum oberen Endes (Q3) der Box beträgt 700 und von Minimum zu Maximum 2000€. Das heißt:
$$IQA = 1900€ – 1200€ = 700€ \quad R = 2800€ – 800€ = 2000€$$

Interpretation
Anhand des Boxplots können wir nun viele Aussagen über die Stichprobe treffen. Q1 beträgt 1200€, somit verdienen 25% der Stichprobe weniger als 1200€ und 75% mehr als 1200€.


Q3 ist 1900€, also verdienen 75% weniger als 1900€ und 25% mehr als 1900€.


Der Median beträgt 1400€, also verdient eine Hälfte weniger, die andere Hälfte mehr als 1400€.



Und die Interquartilsdistanz ist 700€, also liegen die mittleren 50% innerhalb des Intervalls 1200€ bis 1900€.
Das Zeichnen von Ausreißern
Zum Zeichnen von Ausreißern nehmen wir an, die letzte Person unseres Beispiels würde nun 3200€ verdienen. Bis auf das Maximum bleiben die restlichen Lagemaße gleich wie zuvor.
$$x_{MIN} = 800€ \quad x_{MAX} = 3200€ \quad \bar{x}_M = 1400$$
$$Q_1 = 1200 \quad Q_3 = 1900$$
Ein Punkt gilt aus Ausreißer, wenn er mehr als das 1.5-fache des Interquartilsabstand von der Box dh. entweder von \(Q_1\) oder \(Q_3\) entfernt ist.
$$IQA = 1900€ – 1200€ = 700€ \text{ (wie vorher schon berechnet)}$$
Das 1.5-fache des Interquartilsabstand ist damit 1050€.
$$1.5 * IQA = 1.5 * 700 = 1050$$
Die untere Grenze (UG) und obere Grenze (OG) des Intervalls, in dem Werte keine Ausreißer sind, ergibt sich wie folgt:
$$\begin{align}UG &= Q_1 – 1.5*IQA \\ UG &= 1200 – 1050 \\ UG &= 150\end{align}$$
$$\begin{align}OG &= Q_3 + 1.5*IQA \\ OG &= 1900 + 1050 \\ UG &= 2950\end{align}$$
Das Intervall ist also
$$[150€; 2950€]$$
und der Wert 3200€ liegt außerhalb des Intervalls und ist damit ein Ausreißer.

Wir starten mit einem unvollständigen Boxplot.

Als korrektes Maximum müssen wir hier den höchsten Wert nehmen, der noch im gerade ausgerechneten Intervall liegt.

Damit ist der Boxplot bis auf den Ausreißer komplett.

Der Ausreißer wird einfach als Ring auf der gleichen Höhe gezeichnet wie der Rest des Boxplots.

Also so schwer war das ja gar nicht!

Comment (1)
[…] Boxplot zeichnen […]