Tauche ein in unsere modebewusste Statistik-Welt.
Quantile
Hier besprechen wir Quantile. Wir werden lernen,
- … was Quantile sind
- … welche Quantile es gibt
- … wie man sie berechnet
- … wie man sie interpretiert
Da Quantile zu den Lagemaßen zählen, ist es hilfreich, wenn ihr euch schon mit Modus, Median und Mittelwert auseinandergesetzt habt. Wissen zu Skalenniveaus wird hier vorausgesetzt.
Was sind Quantile?
Da Quantile zu den Lagemaßen gehören, kann man sagen, sie beschreiben die zentrale Tendenz. Man kann ein Quantil verstehen, als den Wert einer Verteilung, bei dem ein gewisser Anteil der Daten unterhalb bzw. oberhalb dieses Wertes liegt.
Quantile können bestimmt werden, sobald eure Daten mindestens ordinalskaliert vorliegen.
Das bekannteste Quantil ist der Median. Der Median ist das 50% Quantil. Das bedeutet, dass 50% der Werte in der Stichprobe unterhalb und 50% oberhalb des Medians liegen. Er teilt die Stichprobe also in 2 Hälften.
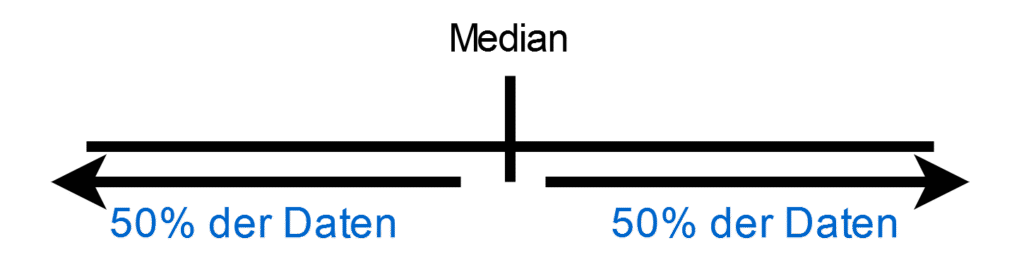
Quantile werden in unterschiedlicher Notation angegeben. Unter anderem so:
$$Q_{\alpha}, \widetilde{x}_{\alpha},x_p \cdots$$
\(\alpha\) beschreibt dabei, wie viel Prozent der Daten links des Quantils liegen. Der Median wäre z. B. \(Q_{0.5}\)
Verschiedene Quantile
Es gibt ganz viele unterschiedliche Quantile.
Die bekanntesten sind die Quartile. Die Quartile \(Q_{0.25}, Q_{0.5},Q_{0.75}\) teilen die Stichprobe in 4 gleich große Abschnitte.
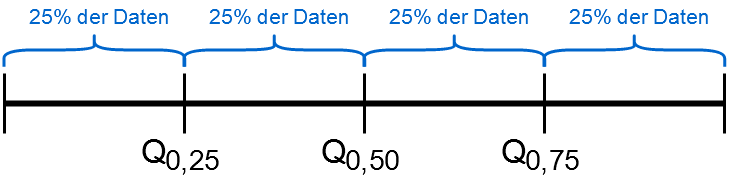
Dann gibt es Quintile \(Q_{0.20}, Q_{0.40}, Q_{0.60},Q_{0.80}\), die die Stichprobe in 5 gleich große Abschnitte teilen.
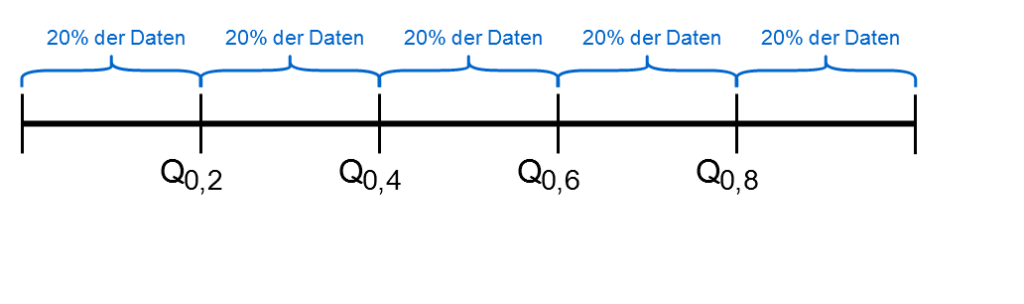
und Dezile \(Q_{0.10}, Q_{0.20}, \cdots ,Q_{0.90}\), die die Stichprobe in 10 gleich große Abschnitte teilen.
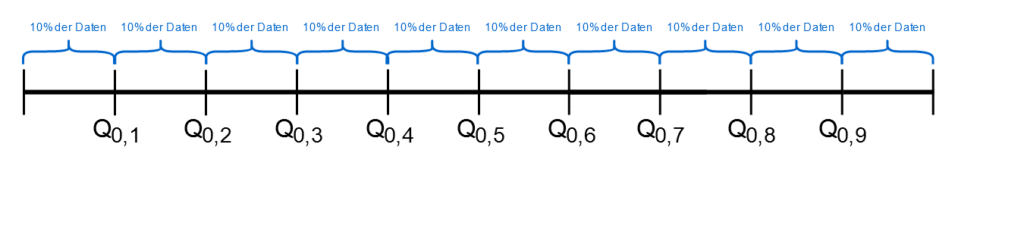
Quintile und Dezile werden des Öfteren zur Unterteilung von Einkommensgruppen verwendet.
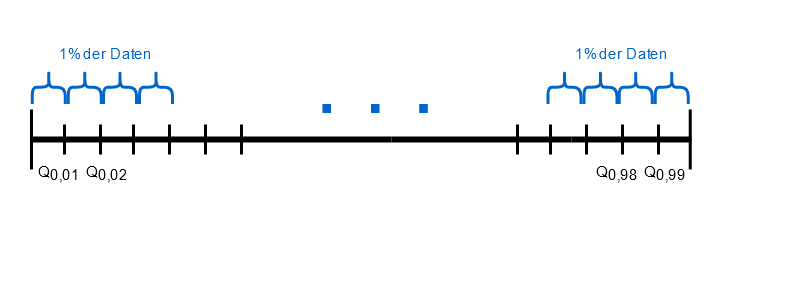
Zudem gibt es auch noch Perzentile \(Q_{0.01}, Q_{0.02}, \cdots Q_{0.99}\). Hier sind die Quantile von 0,01 bis 0,99 in 1% Schritten gemeint.
Quartile
Wie schon beschrieben, teilen Quartile \(Q_{0.25}, Q_{0.5},Q_{0.75}\) die Stichprobe in 4 gleich große Teile.
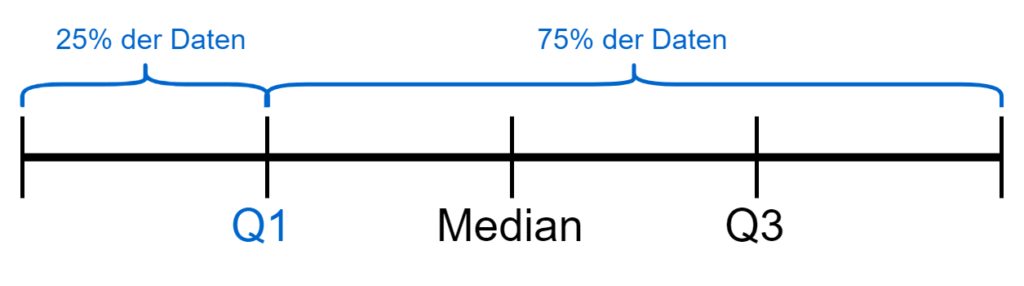
Das 1. Quartil oft einfach nur als \(Q_1\) bezeichnet. Es ist das 25%-Quantil \(Q_{0.25}\). Das heißt also, dass bei dem Wert des 1. Quantil 25% der Daten unterhalb und 75% der Daten oberhalb des Wertes liegen.
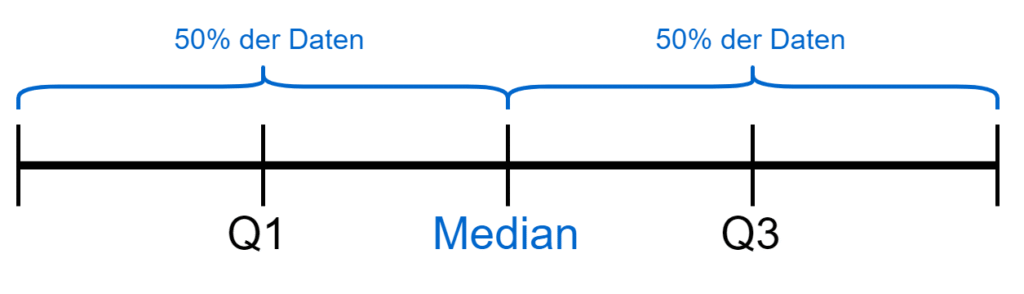
Das 2. Quartil ist das 50% Quantil welches wir bereits als Median kennen.
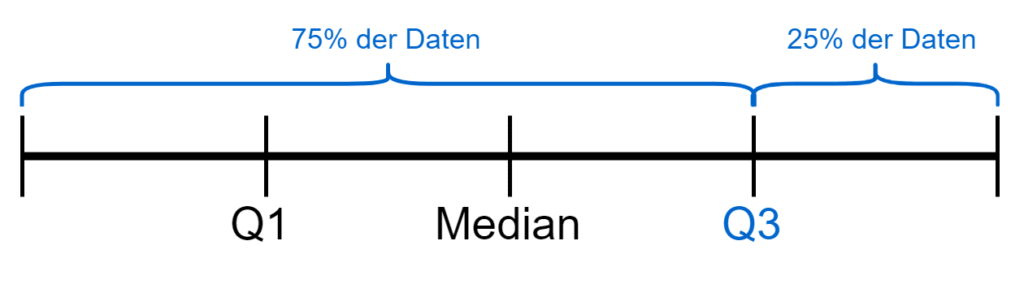
Und das 3. Quartil, also \(Q_3\) bzw. \(Q_{0.75}\), entspricht dem 75% Quantil. Dies bedeutet, dass 75% der Werte unterhalb dieses Quantils und 25% oberhalb liegen.
Achtung: Quantile und Quartile klingen sehr ähnlich, passt also immer auf, von welchem der beiden genau die Rede ist!
Berechnung: Einleitung und Formel
Um uns anzuschauen, wie man Quantile anhand von einfachen Daten berechnen kann, bedienen wir uns wieder den 10 Alterswerten, die wir schon in den Beiträgen zum Modus, Median und Mittelwert als Beispiel herangezogen haben.
$$ 25, 28, 24, 22, 20, 22, 21, 22, 25, 26 $$
Von dieser Stichprobe wollen wir das 20%, 75% und 99%-Quantil bestimmen. Also \(Q_{0.20}, Q_{0.75} \text{und} Q_{0.99}\)
Es gibt eine Formel zur Berechnung von Quantilen:
$$\widetilde{x}_{\alpha} = \begin{cases} x_{\lceil n*\alpha \rceil} & \text{falls } n*\alpha \notin \mathbb{Z} \\ \frac{1}{2} \left( x_{n*\alpha} + x_{n*\alpha+1} \right) & \text{falls } n*\alpha \in \mathbb{Z}
\end{cases}$$
Die Wahl der Formel hängt also davon ab, ob n (= Stichprobenumfang, hier 10) mal dem Quantil \(\alpha\) eine ganze Zahl ist (also in \(\mathbb{Z}\) liegt) oder nicht. Bekommen wir für dieses Produkt eine Kommazahl (nicht Teil der ganzen Zahlen) verwenden wir also die obere Formel, sonst die untere.
Die komisch unfertigen eckigen Klammern \(\lceil \rceil\) bedeuten, dass der Wert in diesen Klammern aufgerundet werden soll. Sie stellen die Ceiling Function dar, falls Ihr davon schon mal etwas gehört habt. Man kann sich leicht merken, dass bei der Ceiling Function aufgerundet wird, da „ceiling“ ja englisch für „Zimmerdecke“ ist.
Würden die Haken der Klammer nach unten zeigen \(\lfloor \rfloor\), müsste man abrunden. Damit würde die Floor Function gemeint sein. (Auch wieder logisch, dass man bei der Floor (= Boden) Function abrundet.)
Diese Formel stellt vermutlich die am häufigsten verwendete Formel zur Berechnung von Quantilen dar. Sie ist aber nicht die einzige!
Es gibt unterschiedliche Berechnungsmöglichkeiten und Quantile werden nicht überall auf die gleiche Art und Weise bestimmt. Das heißt, vielleicht habt ihr im Unterricht etwas anderes gelernt und Statistikprogramme oder auch Excel verwenden oft andere Formen zur Bestimmung von Quantilen.
Berechnung: Anwenden der Formel
Starten wir jetzt also mit der Berechnung des 20% Quantils. Um diese Berechnung durchführen zu können, brauchen wir n und \(\alpha\), welche wir dann multiplizieren.
(\(\alpha\) ist schon gegeben, da die Aufgabe ja ist, das 20% Quantil zu bestimmen. Dementsprechend ist \(\alpha = 0.20\) )
n = 10
\(\alpha\) = 0.2
$$n*\alpha = 10*0.2 = 2$$
Das Produkt von n und \(\alpha\) ist also 2 und damit eine ganze Zahl, weshalb wir die untere der beiden Formeln verwenden.
$$\begin{aligned}\widetilde{x}_{\alpha} &= \frac{1}{2} \left( x_{n*\alpha} + x_{n*\alpha+1} \right)\\ \widetilde{x}_{0.2} &= \frac{1}{2} \left( x_{10*0.2} + x_{10*0.2+1} \right)\\ \widetilde{x}_{0.2} &= \frac{1}{2} \left( x_{2} + x_{3} \right)\end{aligned}$$
Hier stellt \(x_{2}\) den 2. Wert und \(x_{2}\) den 3. Wert der geordneten Stichprobe dar.
Die Werte durchzunummerieren vereinfacht euch das Ganze.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 20 | 21 | 22 | 22 | 22 | 24 | 25 | 25 | 26 | 28 |
Der zweite Wert der Stichprobe ist also 21 und der dritte Wert ist 22.
$$\begin{aligned}\widetilde{x}_{0.2} &= \frac{1}{2} \left( 21 + 22 \right)\\ \widetilde{x}_{0.2} &= \frac{1}{2} \left( 43 \right)\\ \widetilde{x}_{0.2} &= 21.5 \end{aligned}$$
Wir erhalten als 20% Quantil also 21.5 Jahre. Das heißt, 20% der Stichprobe sind jünger und 80% sind älter als 21.5 Jahre. Diesen Wert kann man jetzt auch als das erste Quintil bezeichnen.
Nun weiter zur Berechnung des 75% Quantils, welches, wie ihr jetzt schon wisst, auch drittes Quartil genannt wird.
Wieder bestimmen wir n und \(\alpha\), sowie deren Produkt:
n = 10
\(\alpha\) = 0.75
$$n*\alpha = 10*0.75 = 7.5$$
Das Ergebnist von \(n*\alpha\) ist hier eine Kommazahl, also nicht ganzzahlig. Daher verwenden wir hier, die obere der beiden Formeln.
$$\begin{aligned} \widetilde{x}_{\alpha} &= x_{\lceil n*\alpha \rceil}\\ \widetilde{x}_{0.75} &= x_{\lceil 10*0.75\rceil}\\ \widetilde{x}_{0.75} &= x_{\lceil 7.5\rceil} \end{aligned}$$
Jetzt müssen wir die Ceiling Function \(\lceil \rceil\) auswerten dh. wir runden auf:
$$\begin{aligned}\widetilde{x}_{0.75} &= x_{8}\\ \widetilde{x}_{0.75} &= 25 \end{aligned}$$
Somit entspricht das 75%-Quantil 25 Jahren. 75% sind demnach jünger und 25% älter als 25 Jahre.
Bei der Berechnung des 99%- Quantil bekommen wir für \(n*\alpha\) wieder eine Kommazahl und verwendet demnach diesselbe Formel, wie gerade eben beim 75%- Quantil:
$$\begin{aligned} \widetilde{x}_{0.99} &= x_{\lceil 10*0.99\rceil}\\ \widetilde{x}_{0.99} &= x_{\lceil 9.9\rceil}\\ \widetilde{x}_{0.99} &= x_{10} \\ \widetilde{x}_{0.99} &= 28\end{aligned}$$
Das 99%-Quantil haben wir als 28 Jahre errechnet. Das heißt wieder, dass 99% der Leute in der Stichprobe jünger als 28 Jahre und 1% älter als (bzw. gleich) 28 sind.
Quantile
Hier besprechen wir Quantile. Wir werden lernen,
- … was Quantile sind
- … welche Quantile es gibt
- … wie man sie berechnet
- … wie man sie interpretiert
Da Quantile zu den Lagemaßen zählen, ist es hilfreich, wenn ihr euch schon mit Modus, Median und Mittelwert auseinandergesetzt habt. Wissen zu Skalenniveaus wird hier vorausgesetzt.
Was sind Quantile?
Da Quantile zu den Lagemaßen gehören, kann man sagen, sie beschreiben die zentrale Tendenz. Man kann ein Quantil verstehen, als den Wert einer Verteilung, bei dem ein gewisser Anteil der Daten unterhalb bzw. oberhalb dieses Wertes liegt.
Quantile können bestimmt werden, sobald eure Daten mindestens ordinalskaliert vorliegen.
Das bekannteste Quantil ist der Median. Der Median ist das 50% Quantil. Das bedeutet, dass 50% der Werte in der Stichprobe unterhalb und 50% oberhalb des Medians liegen. Er teilt die Stichprobe also in 2 Hälften.

Quantile werden in unterschiedlicher Notation angegeben. Unter anderem so:
$$Q_{\alpha}, \widetilde{x}_{\alpha},x_p \cdots$$
\(\alpha\) beschreibt dabei, wie viel Prozent der Daten links des Quantils liegen. Der Median wäre z. B. \(Q_{0.5}\)
Verschiedene Quantile
Es gibt ganz viele unterschiedliche Quantile.
Die bekanntesten sind die Quartile. Die Quartile \(Q_{0.25}, Q_{0.5},Q_{0.75}\) teilen die Stichprobe in 4 gleich große Abschnitte.

Dann gibt es Quintile \(Q_{0.20}, Q_{0.40}, Q_{0.60},Q_{0.80}\), die die Stichprobe in 5 gleich große Abschnitte teilen.

und Dezile \(Q_{0.10}, Q_{0.20}, \cdots ,Q_{0.90}\), die die Stichprobe in 10 gleich große Abschnitte teilen.

Quintile und Dezile werden des Öfteren zur Unterteilung von Einkommensgruppen verwendet.
Zudem gibt es auch noch Perzentile \(Q_{0.01}, Q_{0.02}, \cdots Q_{0.99}\). Hier sind die Quantile von 0,01 bis 0,99 in 1% Schritten gemeint.

Quartile
Wie schon beschrieben, teilen Quartile \(Q_{0.25}, Q_{0.5},Q_{0.75}\) die Stichprobe in 4 gleich große Teile.
Das 1. Quartil oft einfach nur als \(Q_1\) bezeichnet. Es ist das 25%-Quantil \(Q_{0.25}\). Das heißt also, dass bei dem Wert des 1. Quantil 25% der Daten unterhalb und 75% der Daten oberhalb des Wertes liegen.

Das 2. Quartil ist das 50% Quantil welches wir bereits als Median kennen.

Und das 3. Quartil, also \(Q_3\) bzw. \(Q_{0.75}\), entspricht dem 75% Quantil. Dies bedeutet, dass 75% der Werte unterhalb dieses Quantils und 25% oberhalb liegen.

Achtung: Quantile und Quartile klingen sehr ähnlich, passt also immer auf, von welchem der beiden genau die Rede ist!
Berechnung: Einleitung und Formel
Um uns anzuschauen, wie man Quantile anhand von einfachen Daten berechnen kann, bedienen wir uns wieder den 10 Alterswerten, die wir schon in den Beiträgen zum Modus, Median und Mittelwert als Beispiel herangezogen haben.
$$ 25, 28, 24, 22, 20, 22, 21, 22, 25, 26 $$
Von dieser Stichprobe wollen wir das 20%, 75% und 99%-Quantil bestimmen. Also \(Q_{0.20}, Q_{0.75} \text{und} Q_{0.99}\)
Es gibt eine Formel zur Berechnung von Quantilen:
$$\widetilde{x}_{\alpha} = \begin{cases} x_{\lceil n*\alpha \rceil} & \text{falls } n*\alpha \notin \mathbb{Z} \\ \frac{1}{2} \left( x_{n*\alpha} + x_{n*\alpha+1} \right) & \text{falls } n*\alpha \in \mathbb{Z}
\end{cases}$$
Die Wahl der Formel hängt also davon ab, ob n (= Stichprobenumfang, hier 10) mal dem Quantil \(\alpha\) eine ganze Zahl ist (also in \(\mathbb{Z}\) liegt) oder nicht. Bekommen wir für dieses Produkt eine Kommazahl (nicht Teil der ganzen Zahlen) verwenden wir also die obere Formel, sonst die untere.
Die komisch unfertigen eckigen Klammern \(\lceil \rceil\) bedeuten, dass der Wert in diesen Klammern aufgerundet werden soll. Sie stellen die Ceiling Function dar, falls Ihr davon schon mal etwas gehört habt. Man kann sich leicht merken, dass bei der Ceiling Function aufgerundet wird, da „ceiling“ ja englisch für „Zimmerdecke“ ist.
Würden die Haken der Klammer nach unten zeigen \(\lfloor \rfloor\), müsste man abrunden. Damit würde die Floor Function gemeint sein. (Auch wieder logisch, dass man bei der Floor (= Boden) Function abrundet.)
Diese Formel stellt vermutlich die am häufigsten verwendete Formel zur Berechnung von Quantilen dar. Sie ist aber nicht die einzige!
Es gibt unterschiedliche Berechnungsmöglichkeiten und Quantile werden nicht überall auf die gleiche Art und Weise bestimmt. Das heißt, vielleicht habt ihr im Unterricht etwas anderes gelernt und Statistikprogramme oder auch Excel verwenden oft andere Formen zur Bestimmung von Quantilen.
Berechnung: Anwenden der Formel
Starten wir jetzt also mit der Berechnung des 20% Quantils. Um diese Berechnung durchführen zu können, brauchen wir n und \(\alpha\), welche wir dann multiplizieren.
(\(\alpha\) ist schon gegeben, da die Aufgabe ja ist, das 20% Quantil zu bestimmen. Dementsprechend ist \(\alpha = 0.20\) )
n = 10
\(\alpha\) = 0.2
$$n*\alpha = 10*0.2 = 2$$
Das Produkt von n und \(\alpha\) ist also 2 und damit eine ganze Zahl, weshalb wir die untere der beiden Formeln verwenden.
$$\begin{aligned}\widetilde{x}_{\alpha} &= \frac{1}{2} \left( x_{n*\alpha} + x_{n*\alpha+1} \right)\\ \widetilde{x}_{0.2} &= \frac{1}{2} \left( x_{10*0.2} + x_{10*0.2+1} \right)\\ \widetilde{x}_{0.2} &= \frac{1}{2} \left( x_{2} + x_{3} \right)\end{aligned}$$
Hier stellt \(x_{2}\) den 2. Wert und \(x_{2}\) den 3. Wert der geordneten Stichprobe dar.
Die Werte durchzunummerieren vereinfacht euch das Ganze.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 20 | 21 | 22 | 22 | 22 | 24 | 25 | 25 | 26 | 28 |
Der zweite Wert der Stichprobe ist also 21 und der dritte Wert ist 22.
$$\begin{aligned}\widetilde{x}_{0.2} &= \frac{1}{2} \left( 21 + 22 \right)\\ \widetilde{x}_{0.2} &= \frac{1}{2} \left( 43 \right)\\ \widetilde{x}_{0.2} &= 21.5 \end{aligned}$$
Wir erhalten als 20% Quantil also 21.5 Jahre. Das heißt, 20% der Stichprobe sind jünger und 80% sind älter als 21.5 Jahre. Diesen Wert kann man jetzt auch als das erste Quintil bezeichnen.
Nun weiter zur Berechnung des 75% Quantils, welches, wie ihr jetzt schon wisst, auch drittes Quartil genannt wird.
Wieder bestimmen wir n und \(\alpha\), sowie deren Produkt:
n = 10
\(\alpha\) = 0.75
$$n*\alpha = 10*0.75 = 7.5$$
Das Ergebnist von \(n*\alpha\) ist hier eine Kommazahl, also nicht ganzzahlig. Daher verwenden wir hier, die obere der beiden Formeln.
$$\begin{aligned} \widetilde{x}_{\alpha} &= x_{\lceil n*\alpha \rceil}\\ \widetilde{x}_{0.75} &= x_{\lceil 10*0.75\rceil}\\ \widetilde{x}_{0.75} &= x_{\lceil 7.5\rceil} \end{aligned}$$
Jetzt müssen wir die Ceiling Function \(\lceil \rceil\) auswerten dh. wir runden auf:
$$\begin{aligned}\widetilde{x}_{0.75} &= x_{8}\\ \widetilde{x}_{0.75} &= 25 \end{aligned}$$
Somit entspricht das 75%-Quantil 25 Jahren. 75% sind demnach jünger und 25% älter als 25 Jahre.
Bei der Berechnung des 99%- Quantil bekommen wir für \(n*\alpha\) wieder eine Kommazahl und verwendet demnach diesselbe Formel, wie gerade eben beim 75%- Quantil:
$$\begin{aligned} \widetilde{x}_{0.99} &= x_{\lceil 10*0.99\rceil}\\ \widetilde{x}_{0.99} &= x_{\lceil 9.9\rceil}\\ \widetilde{x}_{0.99} &= x_{10} \\ \widetilde{x}_{0.99} &= 28\end{aligned}$$
Das 99%-Quantil haben wir als 28 Jahre errechnet. Das heißt wieder, dass 99% der Leute in der Stichprobe jünger als 28 Jahre und 1% älter als (bzw. gleich) 28 sind.

Comment (1)
[…] Quantile […]