Tauche ein in unsere modebewusste Statistik-Welt.
Interquartilsabstand
In diesem Beitrag wird genauer auf den Interquartilsabstand eingegangen.
- Was ist der Interquartilsabstand?
- Berechnung anhand eines Beispiels
Bevor ihr euch diesen Beitrag durchlest, solltet ihr bereits über Quantile, sowie über die Standardabweichung Bescheid wissen.
Was ist der Interquartilsabstand?
Der Interquartilsabstand wird auch Interquartilsdistanz oder auf Englisch Interquartile Range genannt. Er wird deswegen in der Regel entweder als IQA oder IQR abgekürzt.
Man berechnet die Interquartilsdistanz, indem man die Differenz vom dritten zum ersten Quartil bildet.
$$IQA = Q_3 – Q_1$$
bzw. auch
$$ IQA = Q_{0.75} – Q_{0.25}$$
Man nennt die Daten innerhalb dieser Differenz auch ‚die mittleren 50%‚. Beim IQA handelt es sich um ein robustes Streuungsmaß da nicht alle Werte der Stichprobe in die Bewertung einfließen.
Falls ihr euch schon mit Boxplots auskennt, könnt ihr euch merken, dass der Interquartilsabstand der Breite der „Box“ eines Boxplots entspricht.
Beispiel Berechnung
Wir verwenden ein Beispiel, mit dem wir hier bei der Statistikquelle schon gut vertraut sind. Unsere bekannten (geordneten) Alterswerte von 10 Personen:
$$ 20, 21, 22, 22, 22, 24, 25, 25, 26, 28 $$
Der Interquartilsabstand ergibt sich aus einer einfachen Rechnung. Hierfür brauchen wir nur das 3. und 1. Quartil.
Auf die Berechnung der Quartile wird im Beitrag zu Quantilen näher eingegangen.
Das 1. Quantil ist in dieser Stichprobe 22 Jahre und das 3. Quantil ist 25 Jahre.
$$\begin{aligned}Q_1 &= 22\\ Q_3 &= 25\end{aligned}$$
$$\begin{aligned}IQA &= Q_3 – Q_1\\ IQA &= 25 – 22\\ IQA &= 3\end{aligned}$$
Als Ergebnis für den Interquartilsabstand erhalten wir also 3 Jahre.
Interpretation: Das bedeutet, dass die mittleren 50% der Daten innerhalb eines Bereichs von 3 Jahren liegen.
Auf dem folgenden Bild wird der Interquartilsabstand noch visuell (auch im Vergleich zur nicht robusten Spannweite) dargestellt.
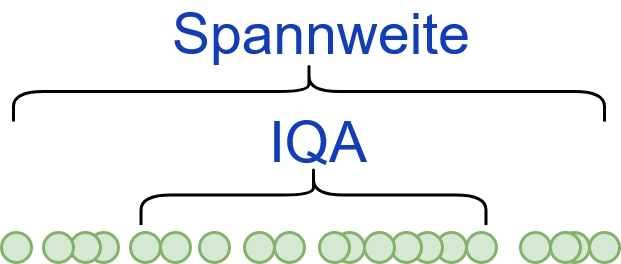
Interquartilsabstand
In diesem Beitrag wird genauer auf den Interquartilsabstand eingegangen.
- Was ist der Interquartilsabstand?
- Berechnung anhand eines Beispiels
Bevor ihr euch diesen Beitrag durchlest, solltet ihr bereits über Quantile, sowie über die Standardabweichung Bescheid wissen.
Was ist der Interquartilsabstand?
Der Interquartilsabstand wird auch Interquartilsdistanz oder auf Englisch Interquartile Range genannt. Er wird deswegen in der Regel entweder als IQA oder IQR abgekürzt.
Man berechnet die Interquartilsdistanz, indem man die Differenz vom dritten zum ersten Quartil bildet.
$$IQA = Q_3 – Q_1$$
bzw. auch
$$ IQA = Q_{0.75} – Q_{0.25}$$
Man nennt die Daten innerhalb dieser Differenz auch ‚die mittleren 50%‚. Beim IQA handelt es sich um ein robustes Streuungsmaß da nicht alle Werte der Stichprobe in die Bewertung einfließen.
Falls ihr euch schon mit Boxplots auskennt, könnt ihr euch merken, dass der Interquartilsabstand der Breite der „Box“ eines Boxplots entspricht.
Beispiel Berechnung
Wir verwenden ein Beispiel, mit dem wir hier bei der Statistikquelle schon gut vertraut sind. Unsere bekannten (geordneten) Alterswerte von 10 Personen:
$$ 20, 21, 22, 22, 22, 24, 25, 25, 26, 28 $$
Der Interquartilsabstand ergibt sich aus einer einfachen Rechnung. Hierfür brauchen wir nur das 3. und 1. Quartil.
Auf die Berechnung der Quartile wird im Beitrag zu Quantilen näher eingegangen.
Das 1. Quantil ist in dieser Stichprobe 22 Jahre und das 3. Quantil ist 25 Jahre.
$$\begin{aligned}Q_1 &= 22\\ Q_3 &= 25\end{aligned}$$
$$\begin{aligned}IQA &= Q_3 – Q_1\\ IQA &= 25 – 22\\ IQA &= 3\end{aligned}$$
Als Ergebnis für den Interquartilsabstand erhalten wir also 3 Jahre.
Interpretation: Das bedeutet, dass die mittleren 50% der Daten innerhalb eines Bereichs von 3 Jahren liegen.
Auf dem folgenden Bild wird der Interquartilsabstand noch visuell (auch im Vergleich zur nicht robusten Spannweite) dargestellt.

