Tauche ein in unsere modebewusste Statistik-Welt.
Stochastische Unabhängigkeit
- Bedeutung
- Beispiele aus dem Alltag – Verständnis
- mathematische Definition
- Prüfung auf Unabhängigkeit (u.a. mit 4-Felder-Tafel)
Für dieses Thema hilft es euch, wenn ihr bereits mit den Axiomen von Kolmogorov, der Laplace Wahrscheinlichkeit und der 4-Felder-Tafel vertraut seid.
Allgemeines
Das Konzept der stochastischen Unabhängigkeit ist ein grundlegendes Element der Wahrscheinlichkeitstheorie. Unabhängige Ereignisse beschreiben Situationen, in denen das Eintreten eines Ereignisses keinerlei Auswirkungen auf ein anderes Ereignis hat.
Ein klassisches Beispiel hierfür ist das Werfen eines fairen Würfels. Die Wahrscheinlichkeit eine 6 zu werfen ist ja bekanntlich 1/6.
$$P(X = 6) = \frac{1}{6}$$
Nehmen wir an, wir haben bereits eine 6 geworfen. Die Wahrscheinlichkeit, erneut eine 6 zu werfen, obwohl ich zuvor schon eine 6 hatte, ist wieder 1/6.
$$P(X_1 = 6 | X_2 = 6) = \frac{1}{6}$$

Was davor passiert ist hat keinen Einfluss auf die Wahrscheinlichkeit des aktuellen Wurfs. Die Wahrscheinlichkeit, eine bestimmte Zahl zu würfeln, ändert sich also nicht, unabhängig davon, welche Zahl zuvor geworfen wurde.
Dasselbe Prinzip gilt auch für eine Münze.
Die Wahrscheinlichkeit für Kopf oder Zahl beträgt jeweils 50%.
$$P(\text{Zahl})=\frac{1}{2} ≈ 50%$$
Selbst wenn ich Zahl erhalte, die Wahrscheinlichkeit im nächsten Wurf erneut Zahl zu werfen ist wieder 50% und nicht höher oder niedriger.
$$P(\text{Zahl} | \text{Zahl}) = \frac{1}{2} ≈ 50%$$

Trotz dieser simplen Erklärung kann das Konzept der Unabhängigkeit für uns Menschen manchmal schwer zu begreifen sein. Daher gehen wir jetzt noch einige Beispiele durch.
Unabhängigkeit anhand eines Münzwurfs
Ein anschauliches Beispiel ist das folgende Münzwurf-Szenario:
Stellt euch vor, wir werfen fünfmal hintereinander Kopf. Wir haben also eine Folge von Münzwürfen und zu einem Zeitpunkt haben wir 5 mal Kopf nacheinander geworfen.
Zum Beispiel: Z, Z, K, Z, K, K, K, K, K …
Intuitiv könnte man denken, dass nun endlich Zahl kommen, die Wahrscheinlichkeit für Zahl somit höher sein müsse. Doch das ist ein Trugschluss. Die Münze „erinnert“ sich nicht an vorherige Würfe – sie ist gedächtnislos. Jeder neue Wurf ist unabhängig von den vorherigen, und die Wahrscheinlichkeit für Kopf oder Zahl bleibt stets 50%.
Unabhängigkeit anhand von Roulette
Ein ähnliches Phänomen kann in Casinos beobachtet werden – besonders beim Roulette. Das Casino zeichnet häufig die vorherigen Ergebnisse auf. D.h. die Zahl und ob die Kugel auf einem roten oder schwarzen Feld gelandet ist, werden aufgezeichnet.

17, 35, 27, 13, 22, 16, 23, 36, 14, 5, 25, … ?
Wenn wir hier einige der letzten Ergebnisse betrachten, sehen wir, dass 6-Mal hintereinander eine rote Zahl gezogen wurde. Wenn mehrmals hintereinander Rot aufgetreten ist, könnt ihr normalerweise beobachten, dass vermehrt auf Schwarz gesetzt wird. Habe ich selbst auch schon gemacht. Aber trotz der Aufzeichnungen hat der Roulette-Tisch selbst natürlich kein Gedächtnis. Die Wahrscheinlichkeit für Rot oder Schwarz bleibt immer dieselbe, unabhängig von vorherigen Ergebnissen.
Unabhängigkeit anhand von Lotto
Dieses Vorgehen lässt sich auch bei anderen Glücksspielen wie dem Lotto beobachten. Dort werden oft akribisch die Zahlen der letzten Ziehungen analysiert, um Trends zu erkennen. Es wird geschaut, welche Zahlen oft und welche weniger häufig vorkamen.
Ausgehend von diesen Analysen wählen dann Personen ihre Zahlen aus, oftmals in der falschen Annahme, dass diese nun eine höhere Wahrscheinlichkeit hätten. Das Prinzip der Gedächtnislosigkeit gilt aber auch in diesem Beispiel und egal wie intensiv man historische Daten analysiert, sie haben keine Auswirkung auf zukünftige Ziehungen.

Zusammenfassung zur Intuition
Es ist faszinierend, wie unser menschliches Gehirn manchmal dazu neigt, Muster und Zusammenhänge zu suchen, selbst wenn sie statistisch nicht existieren. Ist euch das selbst auch schon mal passiert oder habt ihr sowas schon einmal beobachtet? Falls nicht, achtet einmal genauer darauf, wenn ihr ein Brettspiel spielt oder im Casino seid. Ihr werdet möglicherweise bemerken, dass Menschen vermehrt auf eine bestimmte Zahl oder Farbe spekulieren, wenn diese längere Zeit nicht aufgetreten ist.
Zusammenfassend verdeutlicht das Konzept der Unabhängigkeit, dass das Auftreten eines Ereignisses keine Auswirkung auf ein anderes hat; also vergangene Ereignisse keine Vorhersagen für zukünftige Ereignisse liefern können, wenn die Ereignisse unabhängig sind. Es ist wichtig dieses Prinzip zu verstehen, um realistische Erwartungen in Bezug auf zufällige Ereignisse zu entwickeln, besser mit Wahrscheinlichkeiten umgehen zu können und Irrtümer in Bezug auf zukünftige Ereignisse zu vermeiden.
Mathematische Definition
In anderen Beiträgen haben wir bereits den Begriff der bedingten Wahrscheinlichkeit kennengelernt:
\( P(A | B) \) steht dafür, dass wir die Wahrscheinlichkeit von Ereignis A betrachten, unter der Bedingung, dass Ereignis B eingetreten ist. Wenn zwei Ereignisse unabhängig sind, gilt
$$P(A|B) = P(A)$$
Da Ereignis B keine Auswirkung auf die Wahrscheinlichkeit von Ereignis A hat, ist die gesuchte Wahrscheinlichkeit einfach wieder die Wahrscheinlichkeit von A.
Wir sind auch bereits mit dem Multiplikationssatz vertraut, der die Schnittmenge zweier Ereignisse berechnet. Dieser wird mit der Formel \(P(A \cap B) = P(A |B) \cdot P(B) \) beschrieben.
Sind 2 Ereignisse unabhängig, gilt wie oben beschrieben, \(P(A|B) = P(A)\) wodurch der Multiplikationssatz zu folgende wird:
$$P(A \cap B) = P(A) \cdot P(B)$$
Diese Formel, die wir uns soeben hergeleitet haben, wird auch oft als Definition für die stochastische Unabhängigkeit verwendet.
Das wird so formuliert, dass man sagt: Zwei Ereignisse sind unabhängig, wenn gilt \(P(A \cap B) = P(A) \cdot P(B)\).
Beispiel zur Überprüfung von Unabhängigkeit
Wir haben 2 Ereignisse. A stellt das Ereignis dar, dass wir bei einem fairen Würfel eine 1 oder eine 6 werfen und B stellt das Ereignis dar, dass wir eine ungerade Zahl werfen. Sind A und B nun unabhängig?
Definieren wir die Ereignisse und Wahrscheinlichkeiten:
$$A =\{1,6\} \qquad P(A) = \frac{1}{3}$$
$$B = \{1,3,5\} \qquad P(B) = \frac{1}{2}$$
Lediglich der Wert 1 kommt sowohl in A als auch in B vor, daher gilt:
$$ A \cap B = \{1\} \qquad P (A \cap B) = \frac{1}{6}$$
Erste Möglichkeit:
Die Definition der Stochastischen Unabhängigkeit mit der Schnittmenge verwenden und überprüfen, ob die Aussage erfüllt wird.
$$\begin{align}P(A \cap B) &= P(A) \cdot P(B) \\ \frac{1}{6} &= \frac{1}{3} \cdot \frac{1}{2} \\ \frac{1}{6} &= \frac{1}{6}\end{align}$$
Wir erhalten eine wahre Aussage. Die Ereignisse A und B sind also stochastisch unabhängig.
Zweite Möglichkeit:
Wir überprüfen die Definition der Unabhängigkeit mit der bedingten Wahrscheinlichkeit. Diese muss erfüllt sein.
$$P(A | B) = P(A)$$
Mithilfe der Definition der bedingten Wahrscheinlichkeit lösen wir den Ausdruck auf:
$$P(A | B) = \frac{P(A \cap B)}{P(B)} = \frac{\frac{1}{6}}{\frac{1}{2}} = \frac{1}{6} \cdot 2 = \frac{1}{3} = P(A)$$
Die Zweidrittel entsprechen der Wahrscheinlichkeit von A, womit die Unabhängigkeit gezeigt worden ist.
Im zweiten Beispiel wollen wir prüfen, ob die Ereignisse Statistikquelle-Videos-schauen und Statistik-Prüfung-bestehen unabhängig voneinander sind.
S steht für Statistikquelle-Videos-sehen
E steht für Prüfung-erfolgreich-absolvieren
Dazu haben wir die folgende Vierfeldertafel erstellt.
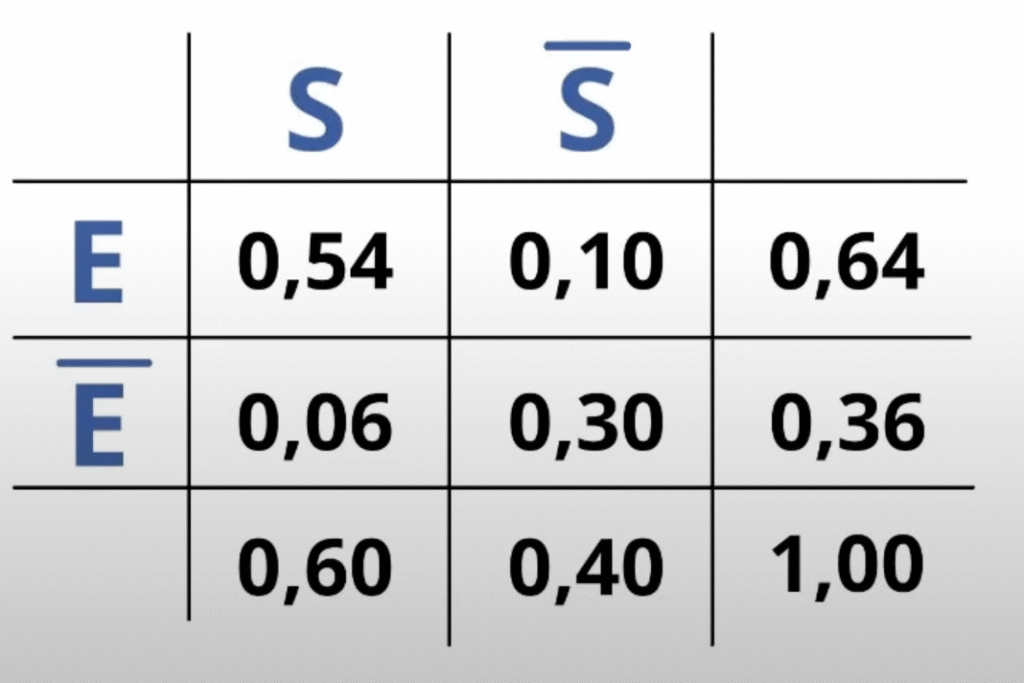
Erste Möglichkeit:
Hier bedienen wir uns wieder der Unabhängigkeitsdefinition mit der Schnittmenge. In diesem Beispiel nehmen wir unsere Ereignisse S und E und setzen in die Formel ein.
$$\begin{align}P(A \cap B) &= P(A) \cdot P(B) \\ P(S \cap E) &= P(S) \cdot P(E) \\ 0.54 &= 0.6 \cdot 0.64 \\ 0.54 &= 0.384 \end{align}$$
0.54 ist gleich 0.384 ist eine falsche Aussage und somit sind die Ereignisse Statistikquelle-Videos-schauen und die Statistik-Prüfung-bestehen stochastisch nicht unabhängig voneinander.
Mit der zweiten Variante können wir das natürlich auch zeigen
$$P(A | B) = P(A)$$
$$P(E | S) = \frac{P(E \cap S)}{P(S)} = \frac{0.54}{0.6} = 0.9 ≠ P(E)$$
Das ergibt dann 0.9 und das entspricht nicht der Wahrscheinlichkeit von E und somit sind die Ereignisse abhängig voneinander.
Stochastische Unabhängigkeit
- Bedeutung
- Beispiele aus dem Alltag – Verständnis
- mathematische Definition
- Prüfung auf Unabhängigkeit (u.a. mit 4-Felder-Tafel)
Für dieses Thema hilft es euch, wenn ihr bereits mit den Axiomen von Kolmogorov, der Laplace Wahrscheinlichkeit und der 4-Felder-Tafel vertraut seid.
Allgemeines
Das Konzept der stochastischen Unabhängigkeit ist ein grundlegendes Element der Wahrscheinlichkeitstheorie. Unabhängige Ereignisse beschreiben Situationen, in denen das Eintreten eines Ereignisses keinerlei Auswirkungen auf ein anderes Ereignis hat.
Ein klassisches Beispiel hierfür ist das Werfen eines fairen Würfels. Die Wahrscheinlichkeit eine 6 zu werfen ist ja bekanntlich 1/6.
$$P(X = 6) = \frac{1}{6}$$
Nehmen wir an, wir haben bereits eine 6 geworfen. Die Wahrscheinlichkeit, erneut eine 6 zu werfen, obwohl ich zuvor schon eine 6 hatte, ist wieder 1/6.
$$P(X_1 = 6 | X_2 = 6) = \frac{1}{6}$$

Was davor passiert ist hat keinen Einfluss auf die Wahrscheinlichkeit des aktuellen Wurfs. Die Wahrscheinlichkeit, eine bestimmte Zahl zu würfeln, ändert sich also nicht, unabhängig davon, welche Zahl zuvor geworfen wurde.
Dasselbe Prinzip gilt auch für eine Münze.
Die Wahrscheinlichkeit für Kopf oder Zahl beträgt jeweils 50%.
$$P(\text{Zahl})=\frac{1}{2} ≈ 50%$$
Selbst wenn ich Zahl erhalte, die Wahrscheinlichkeit im nächsten Wurf erneut Zahl zu werfen ist wieder 50% und nicht höher oder niedriger.
$$P(\text{Zahl} | \text{Zahl}) = \frac{1}{2} ≈ 50%$$

Trotz dieser simplen Erklärung kann das Konzept der Unabhängigkeit für uns Menschen manchmal schwer zu begreifen sein. Daher gehen wir jetzt noch einige Beispiele durch.
Unabhängigkeit anhand eines Münzwurfs
Ein anschauliches Beispiel ist das folgende Münzwurf-Szenario:
Stellt euch vor, wir werfen fünfmal hintereinander Kopf. Wir haben also eine Folge von Münzwürfen und zu einem Zeitpunkt haben wir 5 mal Kopf nacheinander geworfen.
Zum Beispiel: Z, Z, K, Z, K, K, K, K, K …
Intuitiv könnte man denken, dass nun endlich Zahl kommen, die Wahrscheinlichkeit für Zahl somit höher sein müsse. Doch das ist ein Trugschluss. Die Münze „erinnert“ sich nicht an vorherige Würfe – sie ist gedächtnislos. Jeder neue Wurf ist unabhängig von den vorherigen, und die Wahrscheinlichkeit für Kopf oder Zahl bleibt stets 50%.
Unabhängigkeit anhand von Roulette
Ein ähnliches Phänomen kann in Casinos beobachtet werden – besonders beim Roulette. Das Casino zeichnet häufig die vorherigen Ergebnisse auf. D.h. die Zahl und ob die Kugel auf einem roten oder schwarzen Feld gelandet ist, werden aufgezeichnet.

17, 35, 27, 13, 22, 16, 23, 36, 14, 5, 25, … ?
Wenn wir hier einige der letzten Ergebnisse betrachten, sehen wir, dass 6-Mal hintereinander eine rote Zahl gezogen wurde. Wenn mehrmals hintereinander Rot aufgetreten ist, könnt ihr normalerweise beobachten, dass vermehrt auf Schwarz gesetzt wird. Habe ich selbst auch schon gemacht. Aber trotz der Aufzeichnungen hat der Roulette-Tisch selbst natürlich kein Gedächtnis. Die Wahrscheinlichkeit für Rot oder Schwarz bleibt immer dieselbe, unabhängig von vorherigen Ergebnissen.
Unabhängigkeit anhand von Lotto
Dieses Vorgehen lässt sich auch bei anderen Glücksspielen wie dem Lotto beobachten. Dort werden oft akribisch die Zahlen der letzten Ziehungen analysiert, um Trends zu erkennen. Es wird geschaut, welche Zahlen oft und welche weniger häufig vorkamen.
Ausgehend von diesen Analysen wählen dann Personen ihre Zahlen aus, oftmals in der falschen Annahme, dass diese nun eine höhere Wahrscheinlichkeit hätten. Das Prinzip der Gedächtnislosigkeit gilt aber auch in diesem Beispiel und egal wie intensiv man historische Daten analysiert, sie haben keine Auswirkung auf zukünftige Ziehungen.

Zusammenfassung zur Intuition
Es ist faszinierend, wie unser menschliches Gehirn manchmal dazu neigt, Muster und Zusammenhänge zu suchen, selbst wenn sie statistisch nicht existieren. Ist euch das selbst auch schon mal passiert oder habt ihr sowas schon einmal beobachtet? Falls nicht, achtet einmal genauer darauf, wenn ihr ein Brettspiel spielt oder im Casino seid. Ihr werdet möglicherweise bemerken, dass Menschen vermehrt auf eine bestimmte Zahl oder Farbe spekulieren, wenn diese längere Zeit nicht aufgetreten ist.
Zusammenfassend verdeutlicht das Konzept der Unabhängigkeit, dass das Auftreten eines Ereignisses keine Auswirkung auf ein anderes hat; also vergangene Ereignisse keine Vorhersagen für zukünftige Ereignisse liefern können, wenn die Ereignisse unabhängig sind. Es ist wichtig dieses Prinzip zu verstehen, um realistische Erwartungen in Bezug auf zufällige Ereignisse zu entwickeln, besser mit Wahrscheinlichkeiten umgehen zu können und Irrtümer in Bezug auf zukünftige Ereignisse zu vermeiden.
Mathematische Definition
In anderen Beiträgen haben wir bereits den Begriff der bedingten Wahrscheinlichkeit kennengelernt:
\( P(A | B) \) steht dafür, dass wir die Wahrscheinlichkeit von Ereignis A betrachten, unter der Bedingung, dass Ereignis B eingetreten ist. Wenn zwei Ereignisse unabhängig sind, gilt
$$P(A|B) = P(A)$$
Da Ereignis B keine Auswirkung auf die Wahrscheinlichkeit von Ereignis A hat, ist die gesuchte Wahrscheinlichkeit einfach wieder die Wahrscheinlichkeit von A.
Wir sind auch bereits mit dem Multiplikationssatz vertraut, der die Schnittmenge zweier Ereignisse berechnet. Dieser wird mit der Formel \(P(A \cap B) = P(A |B) \cdot P(B) \) beschrieben.
Sind 2 Ereignisse unabhängig, gilt wie oben beschrieben, \(P(A|B) = P(A)\) wodurch der Multiplikationssatz zu folgende wird:
$$P(A \cap B) = P(A) \cdot P(B)$$
Diese Formel, die wir uns soeben hergeleitet haben, wird auch oft als Definition für die stochastische Unabhängigkeit verwendet.
Das wird so formuliert, dass man sagt: Zwei Ereignisse sind unabhängig, wenn gilt \(P(A \cap B) = P(A) \cdot P(B)\).
Beispiel zur Überprüfung von Unabhängigkeit
Wir haben 2 Ereignisse. A stellt das Ereignis dar, dass wir bei einem fairen Würfel eine 1 oder eine 6 werfen und B stellt das Ereignis dar, dass wir eine ungerade Zahl werfen. Sind A und B nun unabhängig?
Definieren wir die Ereignisse und Wahrscheinlichkeiten:
$$A =\{1,6\} \qquad P(A) = \frac{1}{3}$$
$$B = \{1,3,5\} \qquad P(B) = \frac{1}{2}$$
Lediglich der Wert 1 kommt sowohl in A als auch in B vor, daher gilt:
$$ A \cap B = \{1\} \qquad P (A \cap B) = \frac{1}{6}$$
Erste Möglichkeit:
Die Definition der Stochastischen Unabhängigkeit mit der Schnittmenge verwenden und überprüfen, ob die Aussage erfüllt wird.
$$\begin{align}P(A \cap B) &= P(A) \cdot P(B) \\ \frac{1}{6} &= \frac{1}{3} \cdot \frac{1}{2} \\ \frac{1}{6} &= \frac{1}{6}\end{align}$$
Wir erhalten eine wahre Aussage. Die Ereignisse A und B sind also stochastisch unabhängig.
Zweite Möglichkeit:
Wir überprüfen die Definition der Unabhängigkeit mit der bedingten Wahrscheinlichkeit. Diese muss erfüllt sein.
$$P(A | B) = P(A)$$
Mithilfe der Definition der bedingten Wahrscheinlichkeit lösen wir den Ausdruck auf:
$$P(A | B) = \frac{P(A \cap B)}{P(B)} = \frac{\frac{1}{6}}{\frac{1}{2}} = \frac{1}{6} \cdot 2 = \frac{1}{3} = P(A)$$
Die Zweidrittel entsprechen der Wahrscheinlichkeit von A, womit die Unabhängigkeit gezeigt worden ist.
Im zweiten Beispiel wollen wir prüfen, ob die Ereignisse Statistikquelle-Videos-schauen und Statistik-Prüfung-bestehen unabhängig voneinander sind.
S steht für Statistikquelle-Videos-sehen
E steht für Prüfung-erfolgreich-absolvieren
Dazu haben wir die folgende Vierfeldertafel erstellt.

Erste Möglichkeit:
Hier bedienen wir uns wieder der Unabhängigkeitsdefinition mit der Schnittmenge. In diesem Beispiel nehmen wir unsere Ereignisse S und E und setzen in die Formel ein.
$$\begin{align}P(A \cap B) &= P(A) \cdot P(B) \\ P(S \cap E) &= P(S) \cdot P(E) \\ 0.54 &= 0.6 \cdot 0.64 \\ 0.54 &= 0.384 \end{align}$$
0.54 ist gleich 0.384 ist eine falsche Aussage und somit sind die Ereignisse Statistikquelle-Videos-schauen und die Statistik-Prüfung-bestehen stochastisch nicht unabhängig voneinander.
Mit der zweiten Variante können wir das natürlich auch zeigen
$$P(A | B) = P(A)$$
$$P(E | S) = \frac{P(E \cap S)}{P(S)} = \frac{0.54}{0.6} = 0.9 ≠ P(E)$$
Das ergibt dann 0.9 und das entspricht nicht der Wahrscheinlichkeit von E und somit sind die Ereignisse abhängig voneinander.
