Tauche ein in unsere modebewusste Statistik-Welt.
Boxplot
Dieser Beitrag erklärt den Boxplot. Einen detaillierten Beitrag zum Zeichnen eines Boxplots findet ihr hier.
- Erklärung und Anwendung
- Interpretation
- Ausreißer
- Gruppenvergleiche
Um Boxplots gut zu verstehen, solltet ihr vorab unbedingt über Quantile Bescheid wissen. Außerdem ist es hilfreich, wenn ihr auch schon den Interquartilsdistanz und die Spannweite kennt.
Erklärung
Boxplots sind grafische Darstellungen mehrerer Lage- und Streuungsmaße. Sie dienen dazu, sich einen schnellen Überblick über die Daten zu verschaffen.
Sie können bestimmt werden, sobald Daten auf der Ordinalskala oder höher organisiert sind und werden oft auch als Kastendiagramme oder Kastengrafiken bezeichnet. Man kann bei Boxplots die Quartile, die Interquartilsdistanz und die Spannweite ablesen. Sie dienen häufig dem Vergleich mehrerer Gruppen und bei Boxplots lassen sich Ausreißer einfach darstellen.
Was kann man aus einem Boxplot herauslesen?
Wir gehen zuerst auf die Lagemaße ein, die in einem Boxplot enthalten sind. Ein Boxplot zeigt 5 wichtige Werte:
Das Minimum der Daten, das 1. Quartil, den Median aka. 2. Quartil, das 3. Quartil und das Maximum der Daten.
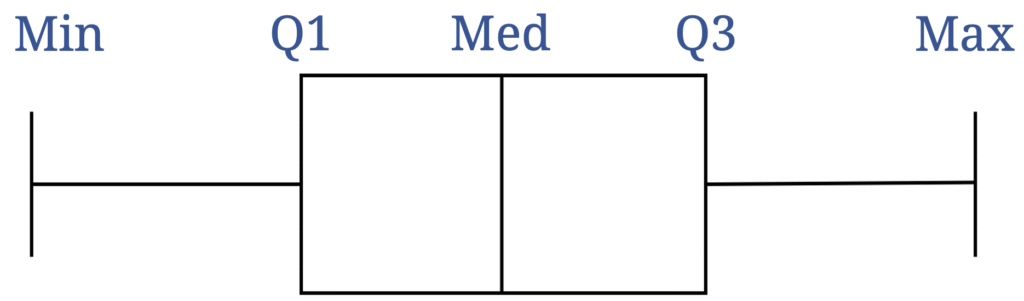
Wie man sieht, befinden sich Minimum und Maximum an den Enden des Boxplots. Die Box beginnt beim ersten Quartil und endet beim dritten Quartil. Der Stich, der die Box in zwei Teile teilt, markiert den Median.
Durch diese Lagemaße erhalten wir auch direkt zwei Streuungsmaße, die man am Boxplot einfach ablesen kann. Und zwar die Differenz von Q1 zu Q3, welche wir als Interquartilsabstand kennen und die Differenz von Minimum zu Maximum, welche die Spannweite darstellt.
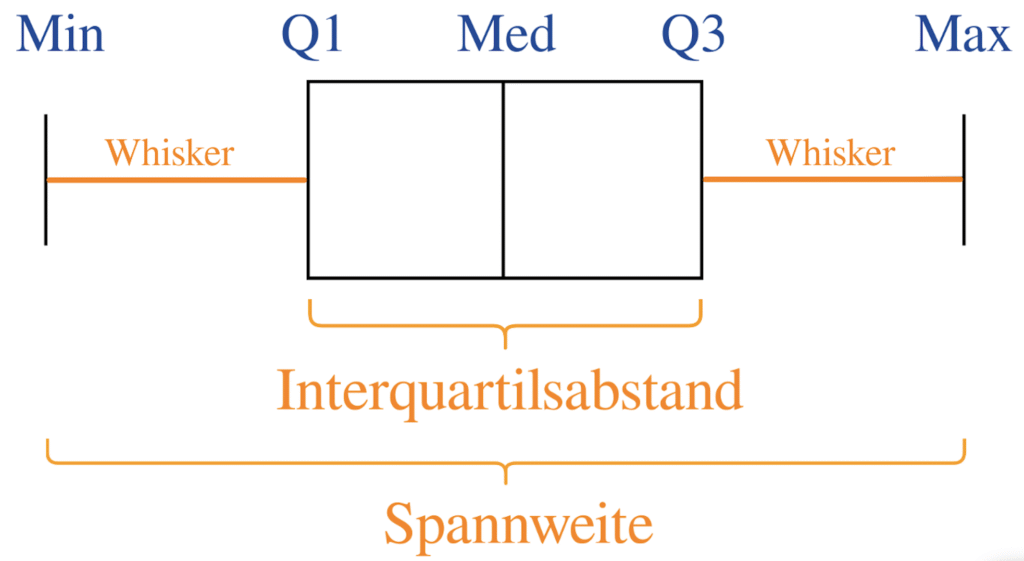
Die beiden Linien außerhalb der Box werden in der Regel als Whiskers bezeichnet.
Dadurch, dass die Box die Quartile zeigt, werden die Daten automatisch in 4 gleich große Teilstücke zu je 25% unterteilt. Egal wie lang oder kurz so ein Abschnitt ist, es befinden sich 25% der Werte der Stichprobe darin.
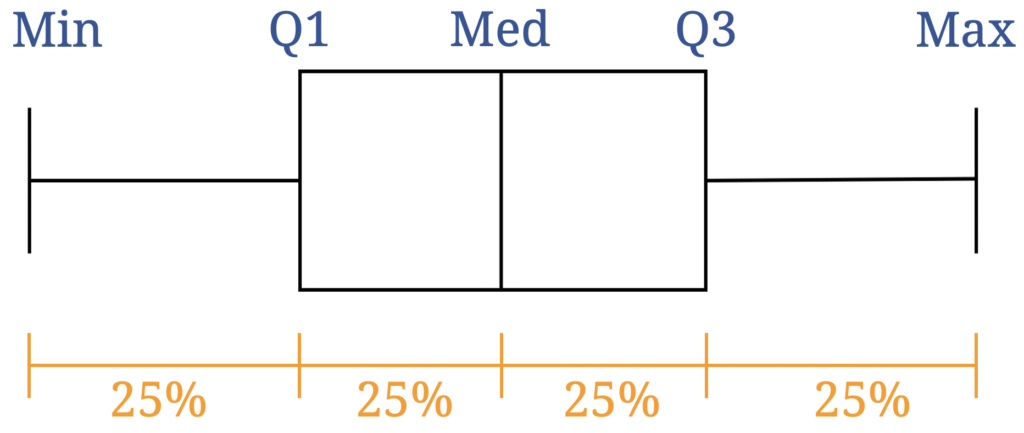
Somit lassen sich sehr viele verschiedene Infos aus einem Boxplot ablesen.
Q1 markiert den Anfang der Box und somit wissen wir, dass 25% der Daten unterhalb dieses Werts liegen und 75% oberhalb.
Dasselbe, aber umgekehrt, gilt für das obere Ende der Box. Dieses zeigt uns nun, dass hier 75% der Daten unterhalb und 25% der Daten oberhalb dieses Punktes liegen.
Der Median teilt die Stichprobe in 2 gleich große Hälften.
Die Interquartilsdistanz zeigt uns, wo die mittleren 50% der Daten liegen.
Es ist übrigens egal, ob ein Boxplot liegend oder stehend abgebildet wird und die zweite Dimension, also ob die Box breiter oder schmaler ist, hat auch keine Aussagekraft.
Achtung
Der Boxplot zeigt uns nur eine Zusammenfassung der Daten. Somit wissen wir nicht mehr exakt, wo die einzelnen Datenpunkte liegen. Außerdem wäre es uns nicht möglich, anhand des Boxplots zum Beispiel Mittelwert oder Standardabweichung zu berechnen.
Ausreißer
Darauf aufbauend sehen wir uns das Thema der Ausreißer an.
Als Ausreißer werden die Werte bezeichnet, die das 1.5-fache des Interquartilsabstands vom nächsten Quartil entfernt liegen. Das heißt, man zieht von Q1 das 1.5-fache des Interquartilsabstands ab und addiert bei Q3 diesen Wert dazu, um die Grenzen der Ausreißer zu bekommen.
Alle Werte außerhalb dieses Intervalls sind dann Ausreißer.
Oft gibt es noch die Unterscheidung, dass ein Wert außerhalb des 1,5-fachen des IQAs als milder Ausreißer und ein Wert außerhalb des 3-fachen der Interquartilsabstands als starker Ausreißer bezeichnet wird.

Den Ausreißer markieren wir mit einem Kringel/ Ring. Fürs Zeichnen von einem Boxplot gibt es einen eigenen Beitrag.
Gruppenvergleiche
Abschließend schauen wir uns noch an, warum man mit Boxplots gut Gruppen miteinander vergleichen kann. Mit Boxplots kann man die Unterschiede bei Lage und Streuung mehrerer Gruppen relativ schnell erkennen. Man nennt diese meist gruppierte Boxplots und sie kommen häufig bei der Varianzanalyse bzw. Anova zum Einsatz.
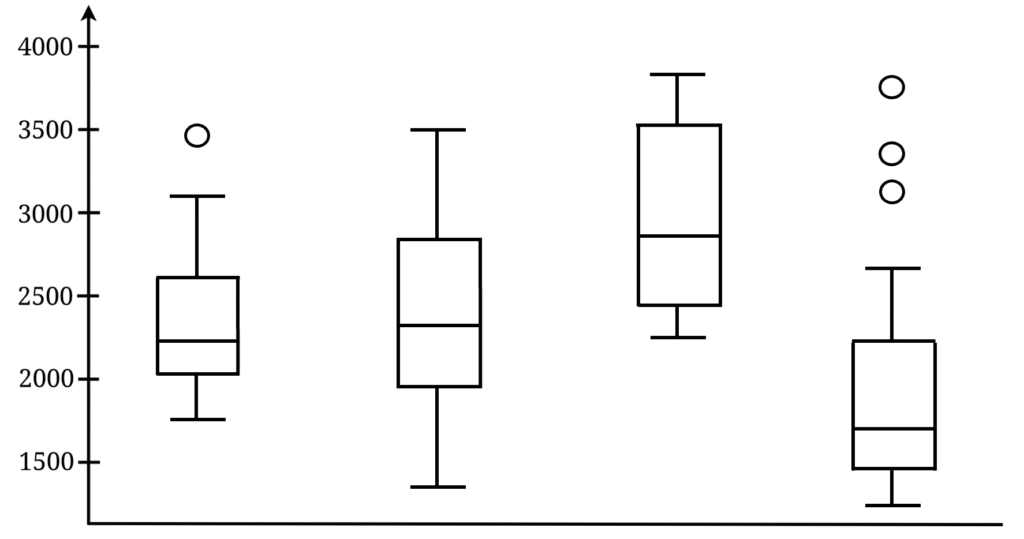
Wir vergleichen hier das Einkommen mehrerer Gruppen miteinander. Die Höhe des Boxplots zeigt uns die Lage der Daten, während die Länge des Boxplots uns Infos zur Streuung gibt.
Wir sehen auf einen Blick, dass die 3. Gruppe im Allgemeinen am besten verdient (weil der Boxplot am höchsten liegt) und die 4. Gruppe am wenigsten (weil dieser Boxplots am weitesten unten liegt). Außerdem erkennen wir, dass es in der 21. Gruppe einen und in der 4. Gruppe drei Ausreißer gibt. Zudem sieht man, dass die Gruppen 1 und 2 mehr oder weniger dieselbe Lage haben, aber die Streuung bei zweiterer deutlich größer ist.
Wie ihr also seht, kann man durch gruppierte Boxplots sehr schnell die Gemeinsamkeiten und Unterschiede in Lage und Streuung verschiedener Gruppen erkennen.
Boxplot
Dieser Beitrag erklärt den Boxplot. Einen detaillierten Beitrag zum Zeichnen eines Boxplots findet ihr hier.
- Erklärung und Anwendung
- Interpretation
- Ausreißer
- Gruppenvergleiche
Um Boxplots gut zu verstehen, solltet ihr vorab unbedingt über Quantile Bescheid wissen. Außerdem ist es hilfreich, wenn ihr auch schon den Interquartilsdistanz und die Spannweite kennt.
Erklärung
Boxplots sind grafische Darstellungen mehrerer Lage- und Streuungsmaße. Sie dienen dazu, sich einen schnellen Überblick über die Daten zu verschaffen.
Sie können bestimmt werden, sobald Daten auf der Ordinalskala oder höher organisiert sind und werden oft auch als Kastendiagramme oder Kastengrafiken bezeichnet. Man kann bei Boxplots die Quartile, die Interquartilsdistanz und die Spannweite ablesen. Sie dienen häufig dem Vergleich mehrerer Gruppen und bei Boxplots lassen sich Ausreißer einfach darstellen.
Was kann man aus einem Boxplot herauslesen?
Wir gehen zuerst auf die Lagemaße ein, die in einem Boxplot enthalten sind. Ein Boxplot zeigt 5 wichtige Werte:
Das Minimum der Daten, das 1. Quartil, den Median aka. 2. Quartil, das 3. Quartil und das Maximum der Daten.

Wie man sieht, befinden sich Minimum und Maximum an den Enden des Boxplots. Die Box beginnt beim ersten Quartil und endet beim dritten Quartil. Der Stich, der die Box in zwei Teile teilt, markiert den Median.
Durch diese Lagemaße erhalten wir auch direkt zwei Streuungsmaße, die man am Boxplot einfach ablesen kann. Und zwar die Differenz von Q1 zu Q3, welche wir als Interquartilsabstand kennen und die Differenz von Minimum zu Maximum, welche die Spannweite darstellt.

Die beiden Linien außerhalb der Box werden in der Regel als Whiskers bezeichnet.
Dadurch, dass die Box die Quartile zeigt, werden die Daten automatisch in 4 gleich große Teilstücke zu je 25% unterteilt. Egal wie lang oder kurz so ein Abschnitt ist, es befinden sich 25% der Werte der Stichprobe darin.

Somit lassen sich sehr viele verschiedene Infos aus einem Boxplot ablesen.
Q1 markiert den Anfang der Box und somit wissen wir, dass 25% der Daten unterhalb dieses Werts liegen und 75% oberhalb.
Dasselbe, aber umgekehrt, gilt für das obere Ende der Box. Dieses zeigt uns nun, dass hier 75% der Daten unterhalb und 25% der Daten oberhalb dieses Punktes liegen.
Der Median teilt die Stichprobe in 2 gleich große Hälften.
Die Interquartilsdistanz zeigt uns, wo die mittleren 50% der Daten liegen.
Es ist übrigens egal, ob ein Boxplot liegend oder stehend abgebildet wird und die zweite Dimension, also ob die Box breiter oder schmaler ist, hat auch keine Aussagekraft.
Achtung
Der Boxplot zeigt uns nur eine Zusammenfassung der Daten. Somit wissen wir nicht mehr exakt, wo die einzelnen Datenpunkte liegen. Außerdem wäre es uns nicht möglich, anhand des Boxplots zum Beispiel Mittelwert oder Standardabweichung zu berechnen.
Ausreißer
Darauf aufbauend sehen wir uns das Thema der Ausreißer an.
Als Ausreißer werden die Werte bezeichnet, die das 1.5-fache des Interquartilsabstands vom nächsten Quartil entfernt liegen. Das heißt, man zieht von Q1 das 1.5-fache des Interquartilsabstands ab und addiert bei Q3 diesen Wert dazu, um die Grenzen der Ausreißer zu bekommen.
Alle Werte außerhalb dieses Intervalls sind dann Ausreißer.
Oft gibt es noch die Unterscheidung, dass ein Wert außerhalb des 1,5-fachen des IQAs als milder Ausreißer und ein Wert außerhalb des 3-fachen der Interquartilsabstands als starker Ausreißer bezeichnet wird.

Den Ausreißer markieren wir mit einem Kringel/ Ring. Fürs Zeichnen von einem Boxplot gibt es einen eigenen Beitrag.
Gruppenvergleiche
Abschließend schauen wir uns noch an, warum man mit Boxplots gut Gruppen miteinander vergleichen kann. Mit Boxplots kann man die Unterschiede bei Lage und Streuung mehrerer Gruppen relativ schnell erkennen. Man nennt diese meist gruppierte Boxplots und sie kommen häufig bei der Varianzanalyse bzw. Anova zum Einsatz.

Wir vergleichen hier das Einkommen mehrerer Gruppen miteinander. Die Höhe des Boxplots zeigt uns die Lage der Daten, während die Länge des Boxplots uns Infos zur Streuung gibt.
Wir sehen auf einen Blick, dass die 3. Gruppe im Allgemeinen am besten verdient (weil der Boxplot am höchsten liegt) und die 4. Gruppe am wenigsten (weil dieser Boxplots am weitesten unten liegt). Außerdem erkennen wir, dass es in der 21. Gruppe einen und in der 4. Gruppe drei Ausreißer gibt. Zudem sieht man, dass die Gruppen 1 und 2 mehr oder weniger dieselbe Lage haben, aber die Streuung bei zweiterer deutlich größer ist.
Wie ihr also seht, kann man durch gruppierte Boxplots sehr schnell die Gemeinsamkeiten und Unterschiede in Lage und Streuung verschiedener Gruppen erkennen.

Comments (2)
[…] Boxplots […]
Beat the Bookmakers with Science — Start Winning Today!
Hello Champion, ⚽
Are you tired of losing bets just because football is unpredictable?
It doesn’t have to be like that anymore…
I offer scientifically optimized betting predictions based on:
✔ probability theory
✔ market deformation analysis
✔ Poisson goal modeling
✔ bookmaker strategic behavior
✔ thousands of real match data points
This is NOT a Telegram channel. NOT a random tipster.
You get direct contact with me — a football analyst and medical scientist with 15+ years of mathematical modeling expertise.
What You Get For Free
Up to 5–7 predictions every Fri–Sun
• 1–3 predictions Mon–Thu
➡ Delivered at least 1 hour before kick-off (confirmed team line-ups)
You pay ONLY if you profit more than 10% ROI for the week.
If there is a negative week — you continue for free until overall profit!
Fair. Transparent. No risk for you.
If a weekly ROI is above +10%, payment is: €7 (bank transfer).
Recent Verified Results
✨ WIN ✨
Chiangmai United 3 – 2 Khonkaen United
Market: 1X • Stake €10 → Profit: +€16.17
✨ WIN ✨
Liverpool 1 – 1 Sunderland
Market: X2 • Stake €10 → Profit: +€33.95
✨ WIN ✨
Sisaket United 1 – 1 Police Tero
Market: Draw • Stake €10 → Profit: +€32.09
❌ LOSS
Fulham 4 – 5 Manchester City
Market: 1X • Stake €10 → –€10.00
Series Summary:
Total Stake: €40.00
Total Profit: €72.21
ROI: +180%
⚽ REAL MATCHES. REAL PROFIT. REAL RESULTS.
Betting Strategy I Recommend
Start with: €100 bankroll
Flat stake: €10 per match
When bankroll reaches €300 → withdraw €180
Keep €120 inside — €20 becomes sacred reserve (never touch it!)
This protects your accounts and grows safety over the year.
To avoid bookmaker limitations:
Maintain accounts at ~10 bookies
Actively bet only at 3
Rotate every 2–3 months
Premium Membership Options
Plan What You Get Price
⭐ Basic Predictions Weekly betting tips only €29/week
Pro System Pack Predictions + Access to my training course + Betting software + LiPad database €247 (one-time)
ELITE VIP Everything above + personal betting assistance + match selection discussion €495 (one-time) + €29/week
Most people choose Pro System Pack —
they learn the system, gain full independence & long-term profit skills.
How to Join
Just reply to this email or message me on one of the apps below
and I will activate your plan within a few minutes.
Contact
Phone / WhatsApp / Viber / Telegram: +359 884 777 799
Global Football Predictions — Smart Betting. Real Results.
Best regards,
Dr. Dimitar Kehayov
Burgas 8000, Lazur District, Block 77, Entrance 11
P.O. Box No. 27 — Bulgaria
Gambling is random.
Strategic betting is profit.